 |
 |
||||||||||||||||||||
     |
|||||||||||||||||||||
Tabla 1 – Los cuatro modelos Dado el carácter epistemológicamente complejo y la tesitura crítica y autocrítica del presente trabajo, conviene establecer desde el principio las metodologías y heurísticas que lo orientan. Ellas configuran el aparato reflexivo del estudio y son fundamentalmente de tres clases. La primera heurística concierne a una tipología de modelos que ya articulé en otros trabajos. Esta tipología, cuyos orígenes se remontan a la idea de complejidad organizada de Warren Weaver (1948), es la que se describe en la tabla 1; la nomenclatura, las propiedades y los propósitos de la clasificación son lo suficientemente claros como para no requerir más comentario. El objetivo de la tipología es demarcar qué clase de resultados cabe esperar de qué clase de modelos (o de qué forma básica de plantear un problema). A diferencia de lo que es rutina en las teorías discursivas o ingenuas de la complejidad, lo que aquí llamo perspectiva no deriva de ni se refiere a las características del objeto real, sea ello lo que fuere; mal que le pese a los antropólogos urbanos o a los que han echado su mirada hacia Occidente o hacia la sociedad (pos)moderna, es una ingenuidad creer que hay sociedades o culturas simples o complejas, u órdenes sociales inherentemente más contemporáneos o más multivariados que otros. Simplicidad y complejidad resultan de aplicar escalas, articular variables o definir focos en el plano epistemológico, y no de cualidades dadas en la realidad. Conforme a las inferencias que ellas aplican y al propósito que se han propuesto, casi todas las teorías a revisarse en este paper pertenecen a los tipos que en la tabla llamo I o II; unas pocas, las más recientes, se inclinan hacia el tipo III. No soy partidario de un tipo en detrimento de otros; cada uno de ellos, incluso el tipo IV, puede ser de aplicación preferencial cuando se plantean los problemas de determinada forma o en determinadas inflexiones de un razonamiento heterogéneo; las investigaciones empíricas en la vida real conmutan, combinan o hibridizan los diversos tipos con o sin autoconciencia de estar haciéndolo. El segundo artefacto que propongo es, como no podría ser de otra manera, una definición de problema. Esta es una criatura conceptual que debería ser de especificación obligatoria en todo texto, pero a la que la epistemología constituida no ha prestado mayor atención. Ni siquiera en la hermenéutica de Hans-Georg Gadamer (1977: 454-455), el primer lugar en el que a uno se le ocurriría buscar, hay el menor rastro de una definición de este tipo. Gadamer especifica cuáles son las propiedades o atributos de un problema: un problema es para él algo que ofende, que choca, que llama la atención; pero no ha definido sustantivamente el concepto. La definición de problema que he hecho mía se origina en la teoría de autómatas y en la tradición de los métodos formales en computación científica: un problema consiste en determinar si una expresión pertenece a un lenguaje (Hopcroft, Motwani y Ullman 2001: 31)2. Abstracta o metafórica como parece, esta cláusula permite evaluar si una expresión (es decir, un caso) es susceptible de ser engendrada por la gramática y/o el conjunto de constreñimientos del lenguaje que se utiliza, entendiendo por ello la teoría, sus operadores y/o sus métodos aplicados a los datos3. Como las ideas de solución y la jerarquía de la complejidad están también embebidas en la cláusula, ésta permite asimismo determinar si un problema es tratable en la forma en que se lo plantea, definir la escala de proporciones entre la pregunta que se formula y los medios instrumentados para contestarla, orientar el modelo de datos, clarificar la naturaleza y evaluar el ajuste del modelado. La definición permite dar cabida tanto a los problemas directos como a los inversos. En los primeros las reglas de producción de la expresión ya se conocen; en el segundo se las debe encontrar o construir. De más está decir que los casos de problemas inversos o de inducción (o abducción) gramatical, aunque implícitos como tales, suelen ser mayoría en la ciencia social empírica, desde las formales a las interpretativas: dado un caso, el investigador procura inducir, conjeturar o modelar las reglas o las coerciones que lo generan. Casi todos los problemas que se relacionan con la interpretación de los datos observados son problemas inversos (Bertuglia y Vaio 2005: 12). Educado en una concepción mecanicista, Jacques Hadamard [1865-1963] consideraba que los problemas inversos son categóricamente problemas mal planteados y que existía una sola solución estable por cada problema (Hadamard 1902; Tarantola 2005). Ya nadie piensa de este modo, pero la distinción entre clases de problemas podría llegar a servir para reflexionar sobre lo que se está haciendo y para definir heurísticas o patrones metodológicos en función de lo que ya se sabe de esas clases. En el ensayo que va a leerse, la definición de problema (directo o inverso) estará siempre activa, como residente en el fondo de la escena, mientras analizo las teorías, describo las propuestas y propongo los instrumentos. La tercera clase de artefactos es un conjunto de criterios epistemológicos. Más allá de los requisitos obvios de correspondencia con los hechos y de consistencia interna, se aplicarán a lo largo de este ensayo tres principios que han demostrado ser útiles en las prácticas de diagnóstico de mi epistemología forense, por así llamarla. Ellos son:
La definición de problema, los cuatro tipos modélicos y los tres principios epistémicos están interrelacionados. En el ejercicio de una crítica teórica o en la evaluación reflexiva de un modelo la definición de problema es el criterio estructural y la condición funcional a satisfacer por los demás elementos, a efectos de que una operatoria que ha puesto en blanco todas y cada una de sus decisiones arbitrarias no degenere en subjetividad o constructivismo: la respuesta a establecer por la definición expuesta debe tender a ser sí o no. La prioridad la tiene la resolución del problema; todo lo demás, con sus libertades y libertinajes inherentes, ha de ser instrumental a ese objetivo. Estas ideas pueden resultar abstractas ahora pero se ilustrarán suficientemente, espero, en el abordaje crítico y metacrítico de las teorías de redes y complejidad que comienzan a examinarse ahora. 3 – Redes, una vez más Predigo que en un futuro no muy
distante la gente Donald Knuth, Things a Computer Scientist Rarely Talks About (1999) Se me ocurren muy pocos asuntos de posible interés en antropología cultural (y casi ninguno en antropología social) que no admitan ser tratados en términos de redes, es decir, en términos de elementos y relaciones entre ellos. Podría pensarse que los conceptos subyacentes a la teoría de redes guardan fuerte relación con principios algo más familiares para los antropólogos como lo son los del estructuralismo, y en particular con la idea estructuralista de sistema, que se define casi de la misma manera. Melvin Whitten y Alvin Wolfe (1973: 719) han advertido esa analogía profunda: “En la década de 1940 –escriben– los penetrantes análisis de [Meyer] Fortes [...] y de [Claude] Lévi-Strauss [...], diferentes como ellos lo son, pusieron tanto énfasis en las intrincaciones de las relaciones socioestructurales que alguna vislumbre de teoría de redes se puede discernir en ellos”. Tan pujante ha sido el modelo de redes en campos como la sociología económica o el modelado sociológico que en esas disciplinas, que no han poseído en su momento a un Lévi-Strauss o conocido un período estructuralista, la metodología constituye el tronco de lo que se ha llamado sociología estructural (Berkowitz 1982; Swedberg 2000). Mientras el estructuralismo languidece en la antropología desde los setenta, Cambridge University Press sostiene desde 1986 una colección de referencia, Structural Analysis in the Social Sciences, dirigida por Mark Granovetter, un teórico mayor que nos ocupará más adelante. Pero a despecho de los nombres que se utilicen en otras disciplinas, el análisis de redes y el estructuralismo no son la misma cosa. Por empezar, la teoría de redes ha sido más cauta que el estructuralismo en muchos respectos; un buen teórico de redes, por ejemplo, nunca afirmaría que toda red califique como sistema sólo por estar constituida como lo está. Y esta es una precaución a tener en cuenta: el hecho de poder representar un conjunto de relaciones como si fuera una red no establece su carácter sistemático ni promueve la indagación a un plano superior de complejidad. Elementos y relaciones, estaba diciendo. Desde el punto de vista semántico los elementos pueden ser cualesquiera (personas, grupos, instituciones, moléculas, piezas de música, palabras, países) y los vínculos también (relaciones de conocimiento, transacciones comerciales, influencia, afinidad, contagio, derivación, violencia, poder, tráfico, relaciones sintagmáticas, clientelismo y por supuesto alianza, filiación y consanguinidad); estos vínculos pueden ser además meramente nominales o finamente cuantitativos. El objetivo del análisis de redes es obtener a partir de los datos relacionales de bajo nivel una descripción de alto nivel de la estructura del conjunto. Los modelos pueden ser tanto estáticos como dinámicos, tanto topológicos como dimensionales, tanto axiomáticos como exploratorios. Aunque se han creado infinidad de medidas (de centralidad de grado, de proximidad, de betweenness; de conglomerado, de conectividad, de diámetro, de cohesión) la teoría de redes no es simplemente cuantitativa; las cuantificaciones de la teoría de redes son menos excursiones en una aritmética envolvente que evaluaciones de la mayor o menor pregnancia de cualidades sumamente expresivas. La representación basada en la metáfora de las redes de ningún modo es más “artificial” que el tratamiento discursivo de una realidad; un poco más abstracto y bastante más visual puede ser, pero no mucho más que eso. En todo caso, la metáfora es tentadora: en una ciencia compleja, la estructura de numerosos modelos de la cosa real puede ser, en ocasiones, algo que podemos pensar en algunos respectos como si se tratara de una red. Como formalismo, la teoría de redes posee una cualidad analógica que la hace particularmente útil e inteligible en ciencias sociales, a juicio de algunos más aún que (por ejemplo) los modelos de simulación. De éstos se ha llegado a decir que deben utilizarse sólo como último recurso allí donde los métodos analíticos han probado ser intratables (Friedkin 2003). El estudio de redes constituye uno de esos métodos analíticos, una especie de modelado down to top que permite pasar de los niveles individuales a las agrupaciones colectivas menos conflictivamente que otros formalismos. Y sí, a veces puede suceder que los modelos planteados sean intratables y haya que intentar otras tácticas. También sucede que el objeto de un modelo de simulación bien podría ser el comportamiento dinámico de una red; y muchas veces se da el caso que las diversas clases de modelos se pueden combinar, algo que en el ambiente de las ciencias complejas está pasando cada vez con mayor asiduidad (Barabási 2003; Amaral y Ottino 2004; Mitchell 2006). El impulso que las teorías de la dinámica no lineal y la complejidad infundieron al análisis de redes puede inferirse de las estadísticas de PubMed (www.pubmed.com) de los últimos años. La figura 1 muestra las cifras correspondientes a artículos que incluyen los nomencladores “network” o “networks” en sus títulos o palabras claves. A comienzos del período contemplado hay un ciclo de crecimiento moderado a caballo de esa Biblia de las formas clásicas del ARS que es el manual de Wasserman y Faust (1994); el punto de inflexión, señalado con una flecha, corresponde al momento de la publicación de los artículos fundamentales de Watts y Strogatz (1998) y Barabási y Albert (1999) y al lanzamiento del programa Ucinet (Borgatti y otros 2002). Duele decirlo, pero al menos en este sistema de indexación en los últimos 4 o 5 años los trabajos sobre redes exceden a los de toda la antropología en su conjunto, la cual no está por cierto experimentando crecimiento alguno de unas décadas a esta parte. 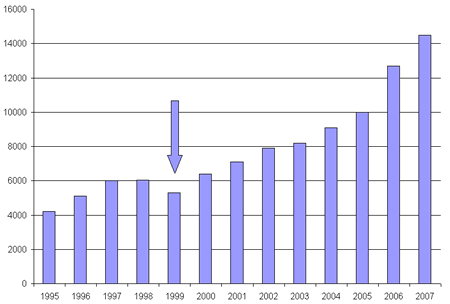Figura 1 – Artículos académicos sobre redes en PubMed (Csermely 2006: 6) En tanto modelo, el formalismo de redes selecciona ciertos aspectos de la realidad y deja de lado otros, pero en esto no hay diferencia entre un tratamiento modelado y otro discursivo. Aún cuando cualitativistas y hermeneutas dejen a veces trasuntar lo contrario, no existen formas naturales de tratar una cuestión; tampoco las hay que sean más humanas o humanizadoras que otras, o que sólo por promover un estilo metodológico o una forma de expresión garanticen ser más profundas, completas, concretas o mejores. En las técnicas de modelado reticulares, igual que en otras clases de modelos, la idea no es reproducir las propiedades de un fenómeno complejo hasta los detalles más mínimos, sino proporcionar resultados acordes con las suposiciones realizadas, permitiéndonos tratar con las implicancias de nuestras opiniones. Si decimos que las relaciones entre sujetos, agentes, actores o lo que fuere tienen tales o cuales características, la analítica de redes permite afrontar algunas consecuencias probables, y en ocasiones deterministas, que se siguen de lo que se postula. Que el vocabulario descriptivo, la semántica de los functores, la emergente lógica espacial de la representación (cf. Aiello, Pratt-Hartmann y van Benthem 2007) y demás elementos del planteo sean públicos –aunque no unánimes– añade otra instancia más de reflexividad. 4 – Momento fundacional: Teoría de grafosLa historia de la teoría de las redes sociales se remonta a los orígenes de la teoría de grafos en matemáticas, creada hacia 1736 por el suizo Leonhard Euler [1707-1783]. Este matemático prodigioso, uno de los escritores más prolíficos de la historia, inventó de la noche a la mañana la teoría de grafos al resolver el famoso problema de los siete puentes sobre el río Pregel en Königsberg, la ciudad que hoy se llama Kaliningrado4. El problema consistía en averiguar si se puede pasar por los siete puentes sin cruzar más de una vez por cada uno de ellos. En su planteamiento, lo que hizo Euler fue como lo que siempre hizo el antropólogo Clifford Geertz sólo que al revés: generalizar el problema. Para ello eliminó de cuajo toda información irrelevante al cálculo de la solución, dejando sólo las masas de tierra, representadas por un punto, vértice o nodo, y los puentes mismos, concebidos como líneas, aristas, bordes o vínculos. La inclinación y longitud de los trazos tampoco son tomadas en consideración. El grafo abstraído por él es lo que hoy se conoce como un multigrafo, un grafo que admite más de un vínculo por vértice. Una red es por cierto una clase de grafo o, formalmente, la interpretación de un grafo (Ore 1962: 2; Bondy y Murty 1976; Harary 1969; Wilson 2004). 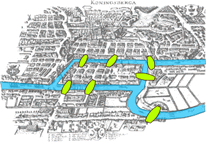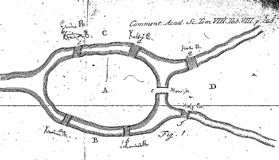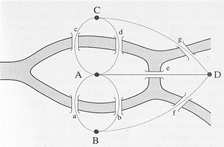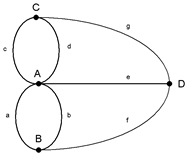Figura 2 – Los puentes de Königsberg/Kaliningrado y su serie de abstracciones De hecho, Euler ni siquiera dibujó un grafo en el trámite de su prueba ni mencionó tampoco esa palabra, que recién fue introducida por James Joseph Sylvester en 1878. Euler llamó grado al número de vértices que convergen en un nodo. La solución solamente considera la distribución de grados en los vértices. El grafo propiamente dicho, ilustrado en la parte inferior de la figura 2 con su notación originaria, fue trazado por vez primera por el matemático inglés Walter William Rouse Ball (1892) a fines del siglo XIX. Euler encontró que la pregunta formulada en el problema de los puentes de Königsberg debía responderse por la negativa. Definió para ello dos conceptos:
Y Euler halló que:
Un grafo con más de dos vértices impares no contiene ningún camino y tampoco contiene ningún circuito de Euler. Siendo que en el caso de los puentes hay tres nodos de grado 3 y uno de grado 5, no hay ningún camino de Euler entre ellos. La lección para los científicos sociales, imbuidos de extremismo idiográfico de un siglo a esta parte, es que estas soluciones son universales y permanentes por cuanto derivan de propiedades inherentes a los respectivos tipos de grafos; no vale la pena pasar noches en vela intentando hallar soluciones alternativas, porque no las hay. En el deslinde de estas propiedades topológicas finca precisamente el origen y el espíritu de la moderna teoría de redes. Figura 3 – Kaliningrado, ca. 1995 – El puente entre A y B De Euler en más (luego de un silencio de más de un siglo) se ha derivado la teoría de grafos, cuyo trámite histórico pasaremos por alto. Basta decir que en ella se distinguen varios estilos y tradiciones, con participación destacada de una escuela húngara (König, Erdös, Rényi, Turán, Gallai, Hajós, Bollobás) que continuará luego en el ámbito aplicativo de las redes, sociales y de las otras (Barabási, Vicsek). Pese a su carácter abstracto, la especialidad que se conoce como la teoría matemática de los hipergrafos, con sus cliques, matroides, árboles y ciclos, ha trabajado en relación con aplicaciones operativas en diversas disciplinas, las redes sociales entre ellas. El concepto de clique, por ejemplo, acuñado en sociología y psicología de grupo, ha ingresado en la terminología matemática formal vinculada a los hipergrafos (Berge 1991: 76, 146, 176; Erdös 1973: 361-362). Las disciplinas empíricas constantemente presentan a las matemáticas problemas de aplicación de los más diversos que, como los puentes de Königsberg, mantienen viva la oferta y la demanda de conjeturas, descubrimientos y pruebas formales. No se trata tanto de que a los matemáticos les interesen los desarrollos aplicativos, sino al hecho de que en la investigación empírica se definen constantemente problemas formales de relevancia que toca a los matemáticos resolver. Si no hubiera surgido el juego de ingenio de caminar por los puentes de Königsberg siguiendo ciertas reglas, tal vez nunca nadie habría pensado que para su resolución conviene pensar en algo tan improbable como un grafo. Consecuencia n° 1: La moraleja epistemológica a sacar de este primer punto en el tratamiento de la teoría de redes es que al menos unos cuantos problemas de la investigación empírica en ciencias sociales podrían abordarse (si es que no resolverse) en función de las propiedades universales de la topología o de la estructura conceptual del fenómeno, antes que en función de los detalles contingentes del caso en particular. Decía Geertz en “Persona, tiempo y conducta en Bali”, escrito en 1966:
Por una vez, el futuro creador del enfoque hermenéutico, con quien casi nunca estoy de acuerdo, ha sabido poner en dedo en la llaga y señalar un criterioso argumento universalista, aunque a su razonamiento puede que le falte una vuelta de tuerca. Cuando él dice que “ciertas clases de estructuras o relaciones” poseen “exigencias de orientación” universales, ello puede suceder no sólo porque ellas sean genéricamente humanas, sino porque resultan congénitos a la naturaleza formal del problema, la cual puede que no implique “una sencilla razón” sino algo bastante más complejo que eso. Que yo haya escogido mi ejemplo de entre las ideas geertzianas no es casual. Lo que pretendo señalar es que en ellas, igual que en otras elaboraciones interpretativas, está faltando una inspección genuina de la naturaleza hermenéutica del problema y de la lógica de la clase de preguntas que en función de esa naturaleza corresponde hacer. A lo que voy en esta primera lección es al hecho de que aún una leve reflexión sistemática sobre los constreñimientos estructurales de un problema ayudaría a evitar falacias recurrentes de la investigación sociocultural. No se necesita echar mano de teoría de redes de última generación para soslayar lo que Jorge Miceli, tomando la idea de la arquitectura de software, ha sugerido llamar “antipatrones” del razonamiento antropológico, pero mi conjetura apunta en esa dirección. Tres breves ejemplos de señalamiento de inferencias incorrectas formalmente evitables vienen aquí a cuento: el principio de Condorcet, el teorema de la imposibilidad de Arrow y la falacia de la personalidad modal de las escuelas de Cultura y Personalidad.
En una palabra, si logramos articular un problema de modo que tenga una estructura de propiedades bien conocida, en muchos casos es posible determinar a priori qué clase de soluciones admite, o si no admite ninguna, o si las que admite son duras de tratar. Aunque en apariencia nos hayamos alejado del centro de la cuestión, el análisis de redes sociales (por la tortuosa vía de la teoría de grafos) alumbra con especial claridad las problemáticas de constreñimiento estructural. Consecuencia nº 2: El corolario más fuerte de la lección de Euler testimonia y exalta la capacidad profundamente humana de la abstracción. Esta tesitura es contraria a la que encontramos en el ya aludido conocimiento local geertziano, en la esfera del conocimiento específico de dominio de varias disciplinas contemporáneas y sobre todo en la resistencia a la abstracción por parte de, por ejemplo, Edgar Morin, quien por un lado cuestiona la hiper-especialización y por el otro sostiene que las ideas generales son ideas huecas y que toda abstracción es mutilante (Morin 1998: 231; 2003: 142). Si algo se aprende con la experiencia de modelado es que las estrategias que denigran la abstracción falsean el hecho que ésta es inevitable: cuando ellas abordan discursivamente un fenómeno, pasan por alto que siempre se está imponiendo a la singularidad de lo concreto el molde arbitrario de las abstracciones de un lenguaje de propósito general, independiente de objeto, contingentemente tipificado. No hay más distorsión en un modelado basado en redes que en una narrativa que trata de embutir la realidad en la jaula del lenguaje. La teoría de grafos y redes no niega ni afirma la legitimidad de otras aproximaciones que alegan ser o que acaso sean más concretas; simplemente destaca nuevas posibilidades de entendimiento basadas en un estilo de abstracción entre los muchos posibles. 5 – De grafos a redes: La Sociometría y la Escuela de HarvardSi esta fuera una historia lineal del pensamiento reticular diríamos ahora que en la década de 1930 un alumno de Gustav Jung, Jacob Levy Moreno [1889-1974], inventó, fundando un campo que él llamo sociometría, algunos formalismos para representar relaciones sociales: sociomatrices y sociogramas. Levy Moreno fue, para decir lo menos, un personaje curioso que creó además el role playing y el psicodrama; admirado por unos y denostado por otros, se lo considera un pensador extravagante y poco digno de confianza, aunque su idea de vincular los grafos matemáticos con las problemáticas sociales haya sido una intuición genial por donde se la mire. Hoy cuesta apreciar la magnitud de su aporte, pero no hay duda que fue sustancial: la sociedad no es un agregado de individuos con sus características, como argüían los estadísticos, sino una estructura de vínculos interpersonales, pensaba Moreno. Más allá de su aparente obviedad, la idea de sociograma no se agota en una representación, sino que explota con inteligencia el hecho de que, al margen de las herramientas de cálculo de las que se disponga, la visión humana está adaptada especialmente al reconocimiento de patrones. No se trata sólo de la vieja leyenda que reza que “una imagen vale más que cien palabras”, una media verdad que depende de cuáles son las imágenes y cuáles las palabras que están en juego; no es en este campo del conocimiento donde mejor prolifera esta clase de lugares comunes. De lo que se trata es del hecho de mucho mayor alcance de las facultades gestálticas, sincrónicas y sintéticas de la visión, capaz de percibir organizaciones imposibles de captar con igual contundencia a través del análisis, el lenguaje o (una vez más) la interpretación. Los primeros sociogramas de Moreno, que se remontan a comienzos de la década de 1930, estaban obviamente dibujados a mano. Sin embargo, en 1934 él ya hablaba en su Who shall survive? de análisis exploratorio, visualización y análisis estructural, términos que ganarían estado público mucho más tarde.
Moreno introdujo al menos cinco ideas claves en la construcción de imágenes de redes sociales: (1) dibujó grafos; (2) dibujó luego grafos dirigidos; (3) utilizó colores para trazar multigrafos; (4) varió las formas de los puntos para comunicar características de los actores sociales; y (5) mostró que las variaciones en la ubicación de los puntos podía usarse para subrayar importantes rasgos estructurales de los datos (Freeman 2000). 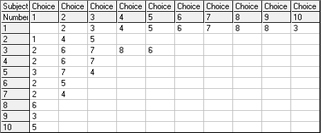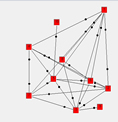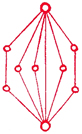Figura 4 – Sociomatriz, sociograma correspondiente y sociograma autógrafo de Moreno La figura 4, realizada con el programa Adit Sociogram®, muestra una sociomatriz y su sociograma correspondiente, al lado de uno de los sociogramas autógrafos más tempranos que se conocen (Moreno 1932: 101). Como sea, Granovetter (1973: 1360) afirma que, encerrada en la psicología social en la que se originó, la sociometría no encontró el camino hacia la sociología; le faltaban las técnicas de medición y muestreo para pasar del nivel del pequeño grupo (un poco más arriba del individualismo metodológico) al plano de las estructuras mayores que haría suyo la Gran Teoría. A instancias de su colaboradora Helen Hall Jennings, en un estudio ulterior publicado en el primer volumen de Sociometry Moreno recurrió al asesoramiento del entonces joven matemático y sociólogo Paul Lazarsfeld [1901-1976]. Esta colaboración resultó en el primer modelo de decisión sociométrico, un modelo probabilístico de un nivel de refinamiento matemático notable para la época (Moreno y Jennings 1938). Próximo a Robert Merton, Lazarsfeld se convertiría con los años en uno de los mayores teóricos de la comunicación de masas; no obstante, sus trabajos no llevan mayormente huellas de los métodos de Moreno y es obvio que en algún momento ambos se distanciaron. En una hipótesis diferente a la de Granovetter, Linton Freeman (2004: 42), uno de los más laboriosos historiadores de la SNA, afirma que la afición de Moreno al misticismo, su estilo personal bombástico y su megalomanía le enajenaron la confianza de sus tempranos partidarios e impidieron que la sociometría hiciera pie en la corriente principal sociológica. El primer gran estudio que he podido localizar que hace uso de métodos sociogramáticos es el clásico de los psicólogos industriales Fritz Roethlisberger y William J. Dickson (1939) sobre las investigaciones en la famosa factoría Hawthorne de la Western Electric en Cicero, Illinois, entre 1927 y 1933. Hawthorne fue un proyecto enorme, impulsado por el fundador del Movimiento de Relaciones Humanas, el australiano Elton Mayo [1880-1949]; renombrado pero mal conocido, constituye la fuente primordial que sirvió años más tarde a Henry Landsberger (1958) para acuñar la expresión “efecto Hawthorne”, esto es, la forma en que la investigación (y en antropología podríamos decir el trabajo de campo en particular) afecta el comportamiento de los sujetos investigados; una definición alternativa es que los participantes de un experimento se comportan distinto si saben que están en una situación experimental. Hay otros nombres que han aplicado a lo mismo o a cosas parecidas: sesgo sistémico, inducción del observador, realimentación epistémica, efecto del experimentador, factores subjetivos, efecto Pigmalión. El efecto Hawthorne, glorificado por algunos y vilipendiado por otros, forma parte de la espesa mitografía de la psicología social y los estudios de motivación en administración de empresas. Los hechos que llevaron a él funcionan como una pantalla proyectiva donde algunos ven simples errores de diseño investigativo y otros un mecanismo de incertidumbre sólo comparable al que impera en el mundo cuántico, capaz de inhibir todo examen formal en ciencias sociales. El asunto es delicado y no pienso que se pueda resolver la disputa en un párrafo cargado de ironías a favor o en contra. Pero la relación entre un diseño investigativo con eventual elicitación de sociogramas y el polémico efecto es en todo caso muy tenue; para mal o para bien, la existencia y naturaleza del efecto mismo ha sido puesta una y otra vez en tela de juicio (Kolata 1998)5. Aunque hacía uso abundante de sociogramas y sociometría, el Movimiento de Relaciones Humanas (y en general la Harvard Business School) no se reconocía tributario de Moreno; sus modelos reticulares fueron elaborados más bien por un antropólogo que había sido discípulo de Radcliffe-Brown en Australia, William Lloyd Warner [1898-1970]. Fue Warner quien convirtió los diseños de investigación de Elton Mayo en estudios de relaciones entre individuos o grupos; también desarrolló las metodologías de proyectos importantes, como los de Deep South, Yankee City y por supuesto Hawthorne. Tanto Warner como Mayo consideraban que sus estudios de grupos constitutían aplicaciones de los modelos estructurales de Radcliffe-Brown. Otras influencias fuertes en la obra de Warner han sido Vilfredo Pareto y Georg Simmel. Suele ignorarse que Warner (1931) fue quien proveyó a Claude Lévi-Strauss los datos sobre la sociedad Murngin explorados en Las estructuras elementales del parentesco; estos datos sirvieron al matemático André Weil [1906-1998], el líder del grupo Bourbaki, para su famoso modelo algebraico (Lévi Strauss 1985: 157, 278-286; Weil 1985).
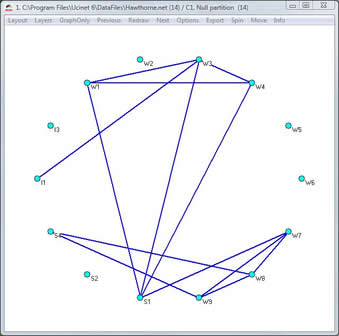
Figura 5 – Sociograma de la factoría Hawthorne De los relevamientos correspondientes a los modelos de Lloyd Warner he tomado los datos para trazar la figura 5, dibujada setenta años después del estudio original usando el programa Pajek. La figura 6, por su lado, se basa en el grafo original que modela la participación de trabajadores (W), soldadores (S) e inspectores (I) en sus discusiones sobre las ventanas de la instalación. Llamo la atención sobre el hecho de que en aquel entonces no existía aún un desarrollo consistente de la teoría de grafos, ni se había fundado el análisis de redes sociales. También fueron dos jóvenes antropólogos, Conrad Arensberg [1910-1997] y Eliot Chapple, salidos del riñón del proyecto Yankee City, quienes aportaron mediciones formales de la interacción y diversas herramientas matemáticas para analizar las ingentes masas de datos recabados en los estudios de Harvard. Chapple (1940) llegó a construir una máquina de escribir especial, llamada “cronógrafo de interacción” para registrar las interacciones mediante observación directa en una especie de rollo de pianola. Tal parece que era un aparato descomunal, impráctico para llevar de campaña, pero que se podía usar en factorías para hacer registros en tiempo real, a medida que la gente interactuaba. En su segundo trabajo importante sobre el tema, Chapple (1953) utiliza explícitamente el concepto de análisis de redes (Freeman 2004: 63). La concepción de Chapple todavía involucraba una extrapolación fisicista; él escribía: “podemos, de hecho, usar una forma modificada de la clase de análisis de redes utilizada en electricidad [...] y podemos determinar los efectos de cualquier cambio en los valores cuantitativos asignados a cualquier vínculo sobre sus vecinos en el patrón reticular” (1953: 304). 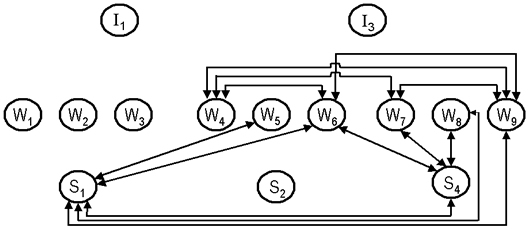Figura 6 – Grafo del proyecto Hawthorne (fig. 40 del original) Una continuación de la sociometría de Moreno de vida relativamente breve fue el programa del Laboratorio de Redes del Instituto Tecnológico de Massachusetts (MIT) conducido por el moreniano Alexander Bavelas desde 1948. El Laboratorio formaba parte del Centro de Investigaciones de Dinámica de Grupos dirigido por el entonces prestigioso Kurt Lewin. Junto a Bavelas, apenas graduado entonces, trabajaban Leon Festinger [1919-1989] y Dorwin Cartwright. Festinger sería luego el creador de la teoría de la disonancia cognitiva, una de las piezas fuertes de la psicología social. Todos los miembros del Lab en el MIT en algún momento ejercieron también influencia en la Escuela de Harvard; ambas instituciones están relativamente próximas en la ciudad de Cambridge, Massachusetts. En este cruzamiento la tradición conservadora de Harvard se benefició del aura de vanguardia del MIT, el cual a su vez recibió algo del prestigio aristocrático de la universidad más vieja de las ocho que forman la rancia Ivy League6. Bavelas, quien había contratado a R. Duncan Luce como su “matemático cautivo”, desarrolló antes que nadie estadísticas de centralidad que todavía integran el repertorio analítico de los principales modelos y de los paquetes de software más utilizados. Bajo guisas muy diferentes, elaborado y vuelto a elaborar una y otra vez, la centralidad es uno de los conceptos fundamentales del análisis de redes y uno de los que mapean con mayores consecuencias las semánticas y magnitudes de las matemáticas sobre las de la sociología y viceversa. Bavelas (1948; 1950) lo utilizaba para explicar el rendimiento diferencial de las redes de comunicación y de los miembros de una red respecto de variables tales como tiempo para resolver problemas, percepción de liderazgo, eficiencia, satisfacción laboral y cantidad de errores cometidos. Desde entonces se ha echado mano de la centralidad como cálculo esencial para afrontar temas de influencia en redes interorganizacionales, poder, posiciones de ventaja en redes de intercambio, oportunidades de empleo, adopción de innovaciones, fusiones corporativas, tasas diferenciales de crecimiento en ciudades y muchos otros (Borgatti y Everett 2006). El único consenso en torno de la categoría es que se trata de una construcción analítica a nivel de nodo. A partir de allí, la centralidad se divide en tres grandes formas de medida: centralidad de grado, de cercanía [closeness] y de betweenness. Al lado de sus aportes estadísticos, Bavelas estabilizó las entonces precarias formas de representación gráfica. En su “modelo matemático para el estudio de las estructuras de grupo”, inscripto en la psicología social y en la antropología aplicada, Bavelas (1948) tuvo la intuición de cambiar la perspectiva geométrica de los mapas de la teoría de campo de Lewin (figura 7, izquierda) por grafos topológicos en los que sólo cuentan las relaciones de vecindad entre las regiones (ídem, derecha). Ese fue un paso más hacia una mayor abstracción y universalidad. Bavelas también generalizó la semántica representacional, confiriéndole la estructura que se conserva hasta hoy. 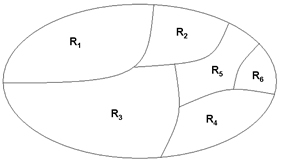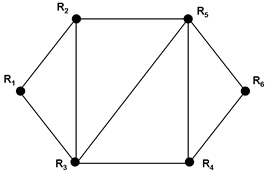Figura 7 – Mapa lewiniano y grafo de Bavelas correspondiente En el plano metateórico, los desarrollos de Bavelas contribuyen a que se puedan comprender mejor las raíces gestálticas de la teoría de campo de Kurt Lewin y los intereses casi emic que lo motivaban; con esta base se puede luego entender más cabalmente la dimensión gestáltica subyacente al régimen visual de la teoría de grafos. Escribe Bavelas:
Colega de los fundadores de la Gestalt (Wertheimer, Koffka, Köhler), Lewin fue también alumno de Carl Stumpf, y de allí los componentes fenomenológicos que todavía se perciben en la formulación de Lewin, una genuina perspectiva del actor de la cual la futura teoría de las redes sociales no tardaría en desembarazarse, pero que subsistiría bajo la forma de las redes centradas en Ego. En 1951 Cartwright formó equipo con Frank Harary, quien tras realizar algunos trabajos sociológicos junto con él, se convertiría poco después en el padre de la moderna teoría de grafos. Esta teoría había sido formulada por el húngaro Dénes König (1931) en una Budapest atribulada por el nazismo, pero fueron Cartwright y Harary (1956) quienes le dieron genuina dimensión sociológica. Con ello su propia sociología pasó de la idea de equilibrio cognitivo a nivel individual a la de equilibrio interpersonal en grupos; a partir de allí fue casi natural que se elaboraran poderosos modelos de cohesión grupal, presión social, cooperación, poder y liderazgo. Dénes König [1884-1944] fue, incidentalmente, el maestro de Paul Erdös. En la línea de König, Harary impulsó no sólo la teoría de grafos dentro del ARS, sino que promovió las matrices (y por ende el álgebra de grupos) como forma de estudiar las relaciones sociales. Hoy en día las estructuras matriciales constituyen la forma primaria de notación de las redes sociales, la materia prima sobre la que operan el análisis y la representación gráfica. De autores como Moreno, Bavelas y Cartwright, así como de las notaciones gráficas de los matemáticos, se derivó la notación que comúnmente se utiliza en teoría de redes sociales. Esta notación es harto más simple que otras convenciones gráficas, como los diagramas de UML, la notación de Forrester, los grafos existenciales o las redes de Petri. Ni siquiera los diagramas de parentesco que los antropólogos memoriosos tal vez recuerden y de las que hablaré luego (no muy bien) eran tan transparentes. Casi se diría que en análisis de redes hay sólo dos clases primarias de entidades (nodos y conexiones) y que cada autor bien puede utilizar los indicadores diacríticos de tipo, peso o direccionalidad que le convenga cuando se lo requiera. 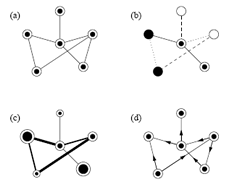Figura 8 – Tipos de redes (grafos) – Basado en Newman (2003: 4) La figura 8 muestra (a) un grafo no dirigido con un solo tipo de vértice y una sola clase de unión, (b) una red con cierto número de tipos y vínculos, (c) una red con diversos pesos de nodos y nexos y (d) un grafo orientado. La versatilidad expresiva y la naturaleza básicamente combinatoria de los grafos les viene de su generalidad. Como decía J. J. Sylvester hace un siglo y medio, “[l]a teoría de la ramificación es de puro co-ligamento, porque no toma en cuenta magnitud o posición; se usan líneas geométricas, pero no tienen que ver con el asunto más que las que se emplean en tablas genealógicas tienen que ver con las leyes de la procreación” (Harary 1969: 1). De más está decir que un modelo de red puede tener información conceptual asociada tan rica como se quiera y que no todas pero unas cuantas tareas analíticas arduas y aburridas pueden hoy resolverse de un soplo (y a bajo costo) poniendo en su lugar tecnologías que ya están ofreciendo más de lo que el común de los investigadores podrá llegar a demandarles. Con ellas no se solucionan todos los problemas inherentes al fenómeno, pero sí se sientan las bases para comenzar a sacar unas cuantas conclusiones que se siguen de la forma en que los hemos planteado y para establecer procedimientos correctivos cuando las tácticas de elicitación o de resolución se manifiestan inadecuadas. Consecuencia n° 3: El desafío que surge de este estado de cosas es que, después de una larga siesta interpretativa y posmoderna, al fin tenemos entre manos un enorme paquete de nuevas técnicas susceptibles de ser comunicadas, enseñadas y aprendidas. Como muy pocos, este paquete se ha convertido en un objeto óptimo de reflexión e intercambio. Se trata de técnicas que crean hábito, y de las que quienes las han probado con algún grado de éxito no encuentran fácil desembarazarse. Con esta idea en mente, cabe preguntarse si, olvidado ya hace décadas el mal llamado método genealógico, los antropólogos de hoy dominan alguna técnica disciplinaria distintiva. Invito a revisar, incidentalmente, la totalidad de las epistemologías de la complejidad de Edgar Morin o de Fritjof Capra para comprobar que en ninguna de ellas se promueve técnica alguna. El corolario que podríamos derivar de este desafío es preguntarse hasta qué punto es razonable que existan teorías que no engendren directa o indirectamente alguna clase de instrumentos, alguna heurística positiva. Esta esterilidad se ha visto antes, por cierto, no sólo en el mundo humanístico sino en la teoría de catástrofes y (dejando a un lado la metodología de Forrester) en la teoría general de sistemas. Pero la situación de vaciamiento ténico en antropología se ha tornado particularmente aguda. Cuando Roy D’Andrade (2000) realizó hace poco un balance de la situación, encontró que los antropólogos ya no están aprendiendo técnicas en su formación académica y que algunas teorías hostiles a las técnicas que se auguraban fructuosas resultaron no serlo. En este sentido, la metáfora de las redes puede re-pensarse como el asiento de un conjunto de técnicas y herramientas que con todas las salvedades del caso permiten poner a prueba su propia pretensión de fecundidad. 6 – Redes aleatorias: Posibilidades y límites del azarMás allá de los avances en teoría de redes propiamente sociales, desde la década de 1950 la teoría matemática de redes experimentó un crecimiento sostenido merced a los trabajos de dos matemáticos húngaros, Paul Erdös [1913-1996] y Alfred Rényi, en contemporaneidad con el hoy olvidado E. N. Gilbert (1959) y con Austin, Fagen, Penney y Riordan (1959). Dado que cuando se trabaja con elementos reticulares, incluso con algunos muy modestos, los problemas se vuelven rápidamente intratables, Erdös y Rényi propusieron considerar modelos probabilísticos, esto es, redes estructuradas estocásticamente, llamadas desde entonces ER por las iniciales de los autores (Erdös 1973: 569). Las “diversas propiedades monótonas” descubiertas en estos modelos son numerosas, pero una de ellas demanda en especial nuestra atención. Me refiero a lo que en la ulterior teoría de la complejidad se ha dado en llamar una singularidad, catástrofe o transición de fase, aunque nuestros autores nunca usaron esos términos. Erdös y Rényi encontraron que cuando el promedio de conectividad de los nodos de una red salta de menos de uno a uno, se pasa de un estado en el cual hay varias redes inconexas a otro estado en el cual se tiene una sola gran red. La figura 9 muestra un ejemplo de red aleatoria de 25 nodos con 18 vínculos contra una del mismo número de nodos y 25 vínculos; en el segundo caso, aunque quedan algunos elementos fuera de la red, la red misma es totalmente conexa, y hay una sola red en el conjunto. Emerge lo que se ha dado en llamar un “componente gigante” (Bollobás y Riordan 2003: 4). La forma de representación escogida de este componente (en el programa Pajek) es un grafo bidimensional en función de la energía según el método propuesto por Thomas Fruchterman y Edward Reingold. Después volveré sobre esta cuestión. 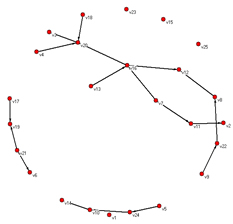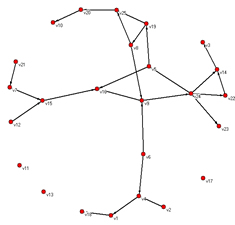Figura 9 – Redes aleatorias, inconexa y conexa Si bien hoy se sabe que en la vida real las redes raras veces poseen la estructura y la dinámica aleatoria de los modelos ER, éstos sirvieron para revelar que en las matemáticas reticulares suceden cosas tales como transiciones abruptas y existen valores tales como puntos críticos que volverán a presentarse en otras clases de redes y en otros universos de fenómenos. El punto crítico es un umbral bajo el cual casi ningún grafo y por encima del cual casi todos los grafos exhiben una propiedad determinada (Diestel 2000: 241). Las transiciones abruptas de los grafos ER se han imaginado análogas a los eventos rápidos de especiación o cladogénesis en las teorías del equilibrio puntuado, un tema apasionante pero demasiado polémico y complejo para tratar aquí. En aquellos años todavía no se hablaba de estas cosas y la súbita demostración de la emergencia de propiedades distintas mediante la evolución monótona de propiedades fue una sorpresa mayor.
Llama la atención que libros austeros plagados de ecuaciones, teoremas, lemmas y corolarios saluden el hallazgo de la transición de fase y su misma naturaleza con palabras alborozadas: un hallazgo sensacional, un espectacular período en la evolución del grafo aleatorio, un fenómeno intrigante, una apasionante época (Janson y otros 2000: 103). El camino para profundizar en estas cuestiones es árido y empinado. La literatura técnica básica sobre redes ER comprende tres de los ocho artículos antológicos de Erdös y Rényi (“Sobre grafos aleatorios I” de 1959, “Sobre la evolución de los grafos aleatorios”7 de 1960 y “Sobre la fuerza y conectividad de los grafos aleatorios” de 1961) que se encuentran en The art of counting (Erdös 1973: 561-617); son ensayos tan densos y ricos que no pocos matemáticos epigonales han hecho carrera con su interpretación. El libro más completo sobre redes aleatorias, de lectura apenas un poco menos prohibitiva, sigue siendo Random graphs de Béla Bollobás (2001). Más accesible y con más sostenida reflexión epistemológica se presenta el artículo “The Erdös-Rényi theory of random graphs” del mismo Bollobás (2002), incluido en el segundo volumen de la compilación de Gábor Halász y otros autores sobre las matemáticas de Erdös. Un volumen por momentos inteligible para científicos sociales es el de Svante Janson, Tomasz Łukzac y Andrzej Rucinski (2000). Una capacidad poco estudiada de las redes y los grafos es su utilidad para el estudio de ritmos bajo un riguroso modelo matemático. Aunque ni los músicos ni los matemáticos han elaborado seriamente el asunto, las redes (los grafos cíclicos, en rigor) son de aplicación inmediata en el análisis y la síntesis del ritmo. Ejemplo de ello son los estudios de Godfried Toussaint (2005), de la Universidad McGill en Montréal, sobre la geometría reticular del ritmo. Paul Erdös (1989), por ejemplo, define como grafos homométricos a aquellos grafos no congruentes cuyos multiconjuntos de las distancias entre pares sean iguales. El problema con las matemáticas es que se refieren a estructuras abstractas y no a las estructuras de la música en particular. Pero ¿qué sucede si aplicamos al modelo una interpretación musical? 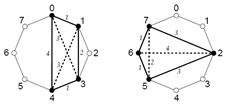Figura 10 – Congas homométricas La figura 10 ilustra los ritmos de conga alta y conga baja, respectivamente, de manera que se puede apreciar su homometría: la suma de los grados de separación de sus acentos y de sus diagonales es igual en ambos casos, ocho y seis respectivamente. Con un programa como Rhythmic Wheels de Ron Eglash, se pueden escuchar los ritmos al cabo de un instante. Aunque el patrón de acentuación es distinto y ni uno solo de sus acentos coincide, ambas variantes se perciben como congas. Mientras se mantengan cuatro nodos y el mismo régimen homométrico habrá una instancia del mismo baile. Es seguro que aparte de las que se muestran en la figura hay otras posibilidades, que dejo al lector buscar. El genio de Erdös y su capacidad de encontrar pautas complejas más allá de la intuición nos permiten comprender un patrón oculto que ni el mejor informante nos habría podido revelar jamás. Rara vez se tuvo antes un modelo de análisis rítmico de semejante elegancia y simplicidad. Incidentalmente, una de las hazañas intelectuales más impactantes de Erdös y Rényi fue su exquisita demostración de la posibilidad de métodos probabilísticos de complejidad moderada (media, varianza, expectativa, principio de inclusión-exclusión y desigualdad de Chebyshev) en la prueba de teoremas deterministas que nada parecían tener que ver con el azar. Aunque no fueron los primeros en examinar las propiedades estadísticas de los grafos, pues el pionero parece haber sido Anatol Rapoport (1957), ellos introdujeron poderosas herramientas de la teoría de la probabilidad en lo que hasta entonces se intentaba resolver mediante recursos de combinatoria enumerativa, acaso un eufemismo para designar el ensayo y error. Hoy en día los métodos en ese renglón son mucho más refinados e incluyen la desigualdad de martingala de Doob, el método Stein-Chen, transformas discretas de Fourier, métodos espectrales, cadenas de Markov de mezcla rápida, desigualdad de Azuma-Heoffding, desigualdades isoperimétricas y muchos más que sería arduo detallar o explicar de qué se tratan, asunto que dejo librado a la inquietud del lector (véase Bollobás 2002: 123). 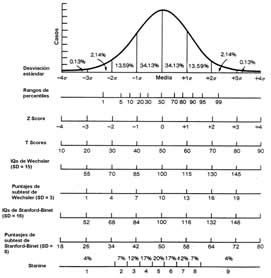Figura 11 – Campana de Gauss y “curva de Bell” Un aspecto importante de las redes aleatorias es que ellas presuponen distribuciones normales o Gaussianas (para mediciones continuas), o distribuciones de Poisson (para mediciones discretas)8. Una forma más adecuada de expresar esto es decir que que la distribución de grados de un grafo aleatorio resulta bien aproximado por distribuciones de esta clase. Una distribución normal característica es, por ejemplo, la de las estaturas de las personas. La clase se caracteriza por mapear en un gráfico de distribución de funciones como una curva en forma de campana, conocida como campana de Gauss, que es lo que se ve a la izquierda en la ilustración de la figura 11. La imagen de la derecha corresponde a la portada de uno de los libros más funestos sobre la presunta distribución normal del aún más presunto coeficiente intelectual, monstruosamente traducido como la “curva de Bell” (Herrnstein y Murray 1994).9 El libro no se refiere a estaturas sino a inteligencia, medida en función de un coeficiente (el de Pearson, el IQ o lo que fuere) que resulta de la unificación de numerosas medidas de escalas disímiles y dependientes de contexto y que presupone correlación positiva entre todas las capacidades intelectuales. A lo que voy es a que una distribución normal presenta una curva en forma de campana cuyo pico coincide con la media y la mediana: una estatura o IQ “normal” es, en este contexto, la estatura o IQ más común en una población; los “normales” son mayoría, como su nombre lo indica. “Todas las distribuciones son normales”, reza el mito: lo mismo me dijo alguna vez el arqueólogo Hugo Yacobaccio cuando todavía no se sabía muy bien que eso (que depende de cómo se construye la muestra y cómo se establecen las escalas) es técnicamente inexacto. La preceptiva estadística de las ciencias sociales presupone erróneamente que esta clase de distribución es dominante; el uso de ese formuleo out of the box para tratar muestras que poseen distribuciones impropias involucra una grave distorsión, comenzando por las mismas operaciones de muestreo. Después volveré sobre estas cuestiones. Es preciso hacer notar una característica de esa distribución: como puede verse en ambas puntas de la curva, siempre hay muy pocos individuos altísimos y muy pocos también de bajísima estatura, o poquísimos genios y gente de poca inteligencia (o como se los llame). La diferencia entre los ejemplares extremos y el pico sería de menguada magnitud: cuatro o cinco órdenes como mucho, jamás del orden de los miles o los millones (Sornette 2006: 94). Dicho de una forma algo más rigurosa, aún en el extremo de aleatoriedad absoluta de una ley gaussiana, las desviaciones de la media mayores a unas pocas desviaciones estándar son muy raras, como si hubiera límites precisos a los grados de libertad del mismo azar. Desviaciones mayores a 5, por ejemplo, nunca se ven en la práctica. Es absolutamente obvio que una entidad caracterizada por este constreñimiento refleja muy pocas características de la vida real. No hay que ponerse en contra de Erdös y Rényi para defender tal extremo. En uno de sus artículos canónicos ellos dicen:
Esta afirmación, incrustada en una de los documentos más circunspectos y refinados de prueba matemática, enseña mucho, a su manera, sobre el carácter, los alcances y los límites del modelado, y sobre la conexión necesaria entre un problema y sus posibles soluciones. Consecuencia n° 4: La lección epistemológica a destilar de estos desarrollos no tiene tanto que ver con el hallazgo sorprendente del umbral de percolación, sino más bien con la noción de tratabilidad, dado que las primeras redes interesantes de la historia se propusieron no porque la naturaleza o la sociedad fueran así, sino porque una red aleatoria no es realista pero es tratable. Vaya concepto. Con todo su espíritu crítico, la antropología, con los posmodernos al frente, se las ingenia para eludir este asunto formidable10. Como si estuvieran escenificando una parodia popperiana, los hermeneutas interpretan y los posmodernos deconstruyen lo que se les ponga por delante de manera absolutamente asertiva sin encontrar nunca límites o impedimentos. Problemas cuya trama (como la del análisis estructural del mito) es órdenes de magnitud más compleja que la Conjetura del Mapa de los Cuatro Colores o que el dilema del Vendedor Viajero, que han sido exasperantemente evasivos para los mejores matemáticos, son atacados por los antropólogos sin casi pensar, sin un solo esfuerzo riguroso de definiciones, sin ningún consenso, con teorías maquinadas en soledad en una noche de insomnio. Pero si trabajamos nuestro material más responsablemente, ¿cómo podemos saber si un problema es tratable, o si es un problema bien formado en primer lugar? Demasiado a menudo el antropólogo presupone que la teoría y el aparato metodológico con que cuenta son suficientes para el abordaje de cualquier problema, sin reflexionar sobre dos cuestiones esenciales: primero que nada, definir qué es un problema, y segundo, determinar que se trate de un problema susceptible de alguna clase de tratamiento en función de la teoría, el método y las técnicas que se es capaz de poner en acción. A diferencia de lo que suponen complejólogos discursivos como Fritjof Capra y Edgar Morin, en este campo del conocimiento la reflexión sobre la tratabilidad nada tiene que ver con los teoremas de Kurt Gödel, los cuales, además de haber sido groseramente malinterpretados y generalizados más allá de ciertas problemáticas de autorreferencia de la aritmética de Peano, tienen muy poco que decir sobre teoría de grafos, métodos probabilísticos, álgebra lineal o su área de influencia (Franzén 2005). En este campo hay multitud de dilemas, pero no precisamente éstos. De treinta años a esta parte, la tratabilidad tiene que ver más bien con la definición de problemas susceptibles (o no) de ser resueltos en tiempo polinómico, lo que ahora se conoce como la problemática de la NP-completitud (Garey y Johnson 1979). Respecto de esta cuestión conviene precisar la terminología. Por empezar, se dice que un problema de decisión pertenece a la clase de complejidad NP si no se conoce una máquina de Turing11 no determinista que pueda resolverlo en tiempo polinómico. Un problema de decisión es NP-duro si cada problema de decisión en NP se puede reducir a él mediante una reducción polinómica de muchos a uno. Los problemas que están en NP y en NP-duros se llaman NP-completos. Reducir significa proporcionar una transformación constructiva que mapee una instancia del primer problema en una instancia equivalente del segundo. Esta transformación brinda los métodos para convertir cualquier algoritmo que resuelve el segundo problema en el correspondiente algoritmo para resolver el segundo (Brandes y Erlebach 2005: 12-13). Para muchos problemas, en efecto, no existe un algoritmo predefinido que facilite su resolución en un tiempo razonable. Pero demostrar que un problema es inherentemente intratable (o NP-completo) es casi tan complicado como encontrar un algoritmo eficiente. En la práctica, la solución a este dilema no es tanto hallar la receta algorítmica perfecta, sino probar que el problema que se tiene entre manos califica como NP-completo, o sea “exactamente igual de duro” que otros que han atormentado a los especialistas por años. Como dicen Garey y Johnson (p. 6), descubrir que un problema es NP-completo equivale a comenzar a trabajar realmente sobre él. En lugar de buscar su solución total, uno se concentrará en otros objetivos menos ambiciosos; por ejemplo, encontrar algoritmos eficientes que resuelvan algunos casos especiales, o que no se pueda probar que corren velozmente pero que se sabe que lo hacen así parte del tiempo, o relajar un poco el problema de modo que se satisfagan solamente algunos de los requerimientos. La teoría de grafos en general y la de redes en particular es un ámbito de excelencia para explorar esta clase de cuestiones; el ejemplo clásico de problema (quizá) NP-completo es el del vendedor viajero [TSP, traveler salesman problem], que muchos reconocerán como una variante del dilema euleriano de los puentes de Königsberg. Las relaciones entre teoría de grafos y teoría de la tratabilidad son estrechas, como la lectura de cualquier buen manual sobre cualquiera de los dos campos permite entrever (Garey y Johnson 1979: 84-86, 131, 194-204; Tamassia 1997). Tal vez mejor dicho: igual que sucede con las relaciones sociales, las cuestiones de tratabilidad se puede abordar mediante grafos. 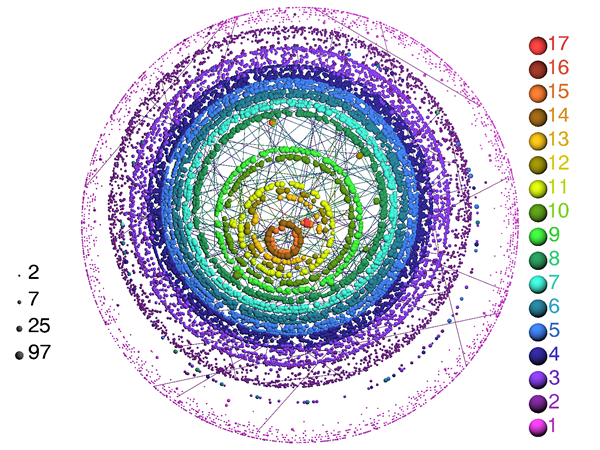Figura 12 – Red de colaboraciones científicas Consecuencia nº 5: Cuando ilustré la evolución de la red aleatoria de inconexa a conexa me referí a una técnica de dibujo de grafos propuesta por Fruchterman y Reingold. Todos los especialistas en redes y usuarios de programas saben que existen otras modalidades de representación (Kamada-Kawai, circular, árbol radial, Bin Pack, GEM, MDS, descomposición k-core). Lo que rara vez se ha explorado es el fundamento de las estrategias de visualización y de sus algoritmos correspondientes; es una pena que así sea, ya que su impacto en la comunicación, expresión y evaluación de los resultados analíticos es palpable. Aquí sólo cabe señalar que la técnica de dibujo de grafos (graph drawing), una rama de la geometría computacional, se ha convertido en algo así como una ciencia aparte con sus congresos separados, una bibliografía superando la cota de las decenas de miles y un consolidado Journal of Graph Algorithms and Applications (http://jgaa.info). La representación de redes complejas ha alcanzado su primer estado de arte, tal como lo prueba la imagen de la figura 12 generada por el programa LaNet-vi que muestra la red de colaboraciones científicas sobre física de la materia condensada entre 1995 y 1998 en base a datos elaborados por Mark Newman de la Universidad de Michigan. El tamaño de cada nodo corresponde a la escala ascendente de su grado (del violeta al rojo, como el espectro del arco iris) y el color a su coreness. Aún a simple vista se trata, perceptiblemente, de una red libre de escala, un concepto de importancia crucial que se revisará más adelante. Pero más allá de la excelencia tecnológica, esta problemática trae a la mente la cuestión de las metáforas (formas laxas, cualitativas, densamente estéticas) que son capaces de inspirar modelos. No se puede menos que pensar en Victor Turner o en Clifford Geertz y en sus metáforas de la cultura como texto, como drama, como juego. Algunos de los algoritmos de dibujo de grafos se inspiran, efectivamente, en superposiciones de densas metáforas imaginales y transdisciplinarias; el de Fruchterman y Reingold (1991), por ejemplo, establece fuerzas de atracción y repulsión entre nodos conforme a una ley de potencia gravitacional, se atiene a la ley de Robert Hooke [1635-1703] formulada en tiempos de Newton sobre el comportamiento macroscópico de los resortes y restringe los movimientos del grafo a medida que corre el tiempo de acuerdo con la heurística de simulación de templado de metales, la cual he descripto en otra parte (Reynoso 2006: 225). Es obvio que en teoría de redes sociales y en antropología en general todavía no se ha razonado con detenimiento sobre esas metáforas. En algún momento habrá lugar para una fenomenología de la percepción visual en ciencia, acaso en la línea de un Merleau-Ponty con un toque formal; un estudio semejante aplicado a la visualización de redes y grafos está haciendo falta aquí y ahora. Más que conocimiento matemático de rutina o normativas ciegas, lo que ha alimentado las mejores intuiciones en técnicas complejas de dibujo de grafos ha sido la imaginación creativa, la erudición literaria y la captación de pautas que conectan. Definitivamente, la técnica ha dejado de ser un juguete ilustrativo para constituirse en instrumento metodológico por derecho propio (Bender-deMoll y McFarland 2006). Por más que sea un antropólogo inclinado a la semántica y a las estrategias cualitativas (y sobre todo en ese caso) el lector hará bien en echar un vistazo a la bibliografía referida al asunto para tomar noticia de las complejas relaciones entre el significado, la representación y la percepción de patrones que se trabajan en otras ciencias (Di Battista y otros 1999; Tamassia 1999; Nishizeki y Rahman 2004); en algún campo de casi todas las otras ciencias, para ser más precisos. 7 – Teorías sociológicas y antropológicas de redesAunque la historia es más compleja que eso, se dice habitualmente que en teoría de redes tradicional hay una corriente sociocéntrica que viene de la sociología y se remonta a Georg Simmel [1858-1918] y una tendencia egocéntrica que floreció en antropología social y que se deriva a la larga de Alfred Reginald Radcliffe-Brown [1881-1955] y sus ideas sobre la estructura social con sus “tejidos”, “texturas” o “tramas” (véase Freeman 1982; Scott 2000; Martino y Spoto 2006; Freeman 2004; De Nooy, Mrvar y Batagelj 2005: 123, 144). Fue Radcliffe-Brown, el padre del estructural-funcionalismo, quien escribió tan temprano como en 1940 que la estructura social australiana se basaba en una “red” de relaciones diádicas de persona a persona (según Wolfe 1978). A comienzos de la década siguiente llegó a escribir que “los seres humanos están conectados por una compleja red de relaciones sociales. Utilizo el término ‘estructura social’ para denotar esta red de relaciones realmente existentes” (Radcliffe-Brown 1965: 190). En cuanto a Simmel, él es uno de esos autores intensamente discursivos cuyos libros, de pertenencia disciplinaria incierta, se traducían y frecuentaban muchísimo medio siglo atrás pero que poco a poco se han dejado de leer. Sin duda habría que leerlo de nuevo pues su rara escritura, carente de todo razonamiento explícitamente matemático, es paso a paso una invitación al modelado basado en imágenes, como cuando dice:
Aunque Simmel ha anticipado exactamente problema de las redes grupales, proponiendo en pleno siglo XIX estudiar el poder y las jerarquías, escribiendo sobre el tejido de las afiliaciones de grupo (1966 [1922]), inventando nociones tales como díadas y tríadas [Zweierverbindung, Dreierverbindung], la historia de la modalidad sociocéntrica es bien conocida y no malgastaré tiempo y espacio volviéndola a contar. Es la crónica olvidada de la dimensión teorética de la antropología de redes (no necesariamente su historia, ni el resumen de sus estudios empíricos) la que vale la pena recordar ahora. En contemporaneidad con desarrollos matemáticos fundamentales, la escuela de Manchester liderada por Max Gluckman constituyó durante unos veinte años (entre 1955 y 1975, digamos) una alternativa opuesta a los planteamientos sincrónicos y estáticos de la antropología sociocultural inglesa, de tono estructural-funcionalista. Es en la escuela de Manchester, una institución de pequeña envergadura, donde se hicieron los primeros aportes británicos a la antropología urbana, se propusieron teorías de la dinámica y el cambio y se usaron por primera vez redes antropológicas. Algunos de los vectores iniciales de influencia fueron las ideas de Siegfried Nadel [1903-1956], quien desarrolló una teoría plasmada en su libro póstumo The theory of social structure (1957) que él no llegó a elaborar en términos de redes pero que luego otros usaron como inspiración para hacerlo. Nadel conocía muy bien las teorías gestálticas de Köhler y de Lewin y sostenía que para llevar adelante un análisis del rol había que implementar métodos algebraicos y matriciales. Afirmaba Nadel, citando aquí y allá a los Ensayos de Talcott Parsons:
Suele ignorarse que el uso de álgebras relacionales en ARS debe mucho a las definiciones que Nadel propuso para el rol social. Junto con las propuestas de Robert Merton, son las que mayor influencia han tenido en el desarrollo de las metodologías reticulares de rol (Wasserman y Faust 1994: 426). Nadel deriva su definición de manera explícitamente relacional, puesto que la fundamenta en las regularidades o en los patrones de relaciones entre individuos. Su elaboración estuvo a un paso de ser un marco de referencia de teoría de conjuntos, en el cual la estructura interna de los roles se consideraba una colección de atributos de rol. Aunque los expertos en ARS sostiene que su marco no tiene la precisión analítica suficiente para permitir un análisis de redes formal sin más trámite, recuperan el hecho de que haya puesto el foco en “la interrelación o el entretejido de las relaciones (Nadel 1957: 17), un rasgo clave en los modelos formales de rol. También pueden percibirse ideas claramente reticulares en uno de los libros anteriores de Nadel, The foundation of social anthropology (1951); en su escritura se echan de menos por cierto las representaciones gráficas, las cuales, alimentándose en forma directa y en tiempo real de los textos iniciales del padre de la moderna teoría de grafos Frank Harary [1921-2005], radicado en Estados Unidos, llegarían a la antropología manchesteriana por vía libresca poco después (cf. Nadel 1974: 89-97; Harary 1969). El modelo de Manchester, llamado a veces antropología interaccional, enfatizó las redes centradas en Ego (o redes personales) constituidas a nivel urbano. Estas redes fueron diferenciadas y propuestas por James Clyde Mitchell [1918-1995] miembro fundador del INSNA y de su revista Connections, inspirándose en el método genealógico creado por W. H. R. Rivers hacia 1898, en ocasión de la expedición de la Universidad de Cambridge al Estrecho de Torres en la que se sentaron las bases del trabajo de campo profesional (cf. Mitchell 1969; 1974). De todos los manchesterianos, Mitchell fue el que utilizó modelos matemáticos con mayor nivel de refinamiento. También fue, junto con Barnes (1954: 43; 1969), uno de los que prestó atención a sus grafos y matrices, mientras que otros (como Norman Whitten) a duras penas mencionan grafos como tales. El creador del concepto de red social fue el antropólogo John Barnes (1954), quien promovió el pasaje de una concepción metafórica a una afirmación conceptual sobre relaciones sociales. El uso metafórico de la palabra enfatiza que existen vínculos sociales entre individuos que se ramifican a través de la sociedad. El uso analítico de la idea, que es el que aporta Barnes, pretende especificar de qué manera esta ramificación ejerce influencia en el comportamiento de la gente involucrada en una red. Barnes desarrolló la idea de red como consecuencia de su descontento con el marco categorial del estructural-funcionalismo entonces menguante pero todavía en vigencia. Escribía Barnes:
El aporte fundamental de Barnes, vivo hoy en día como nunca antes, se asentaba en la convicción de que los métodos del ARS proporcionaban afirmaciones de carácter formal referidas a atributos y procesos sociales. Estos conceptos se pueden definir con alguna precisión, permitiendo razonar formalmente sobre el mundo social (Freeman 1984; Wasserman y Faust 1994: 11). Conceptos históricos de la antropología, la sociología y la psicología social como grupo o rol social se ven ahora, mientras no exista una definición clara en términos de redes, como “conceptos sensibilizadores” de alcance limitado. A partir de allí, casi todos los teóricos de redes están de acuerdo con Samuel Leinhardt (1977: xiv) en el sentido de que “no es posible construir teorías explicativas satisfactorias utilizando metáforas”. Muchos de los conceptos formales del ARS se derivan de esa convicción, como los de densidad (Bott 1957), span (Thurman 1980), connectedness, clusterability y multiplexity (Kapferer 1969). En sus trabajos de la década de 1960, Barnes se preocupó por precisar el lenguaje de discusión sobre redes, recurriendo intensamente a conceptos de la teoría de grafos que por aquel entonces se estaba codificando. Penetrando en el espacio abstracto de la representación de las redes totales, Barnes trató de establecer las claves de las redes parciales. Habiendo definido la red total como coincidente con la idea de “sociedad” y las redes parciales con dominios particulares de la sociedad (parentesco, política, intercambio) partió de abajo hacia arriba, desarrollando conceptos que hacían referencia a redes sociales centradas en Ego: alfas, contactos, estrellas, zonas de primero y segundo orden, etcétera. Aquí comienzan a visualizarse tanto promesas como peligros latentes. Escriben Whitten y Wolfe:
La primera trilogía de estudios antropológicos basados en redes, incluyendo el de Barnes, el de Elizabeth Bott (1957) y el de Philip Mayer (1961), no revelan gran cosa sobre la elicitación de redes en el trabajo de campo; observando el hiato temporal entre la experiencia de campaña y la aparición de diversos elementos de juicio en modelado matemático, por ejemplo, se advierte que la metodología fue adoptada más tarde en el gabinete y no definida como parte del diseño primario de la investigación. Algo llamativo es también que ninguno de los estudios clásicos de redes en el período de la primera Edad de Oro antropológica (entre 1954 y 1974) se ocupa de sociedades en pequeña escala. Aunque algunos de ellos corresponden a campañas africanas, siempre se trata de ciudades y no de aldeas, y siempre de asuntos contemporáneos antes que de las tradiciones arcaicas. La codificadora reconocida de la clase de redes propuesta por Barnes fue la psicóloga canadiense Elizabeth Bott (1957), quien había estudiado con Lloyd Warner en Chicago y conocía de cerca la obra de Lewin y de Moreno. Bott pensaba que en la medida en que Ego estuviera fuertemente ligado a otros a su vez ligados entre sí, todos tenderían a alcanzar consenso y a ejercer presión informal pero consistente sobre el resto para alcanzar conformidad con las normas, estar en contacto mutuo y de ser preciso ayudarse entre sí; en el otro extremo, si los vínculos fueran esporádicos, esa consistencia normativa resultaría más improbable. La hipótesis principal alega que la clase de red en que la familia está inserta afecta de manera muy directa las relaciones de rol conyugal en esa familia: una red estrechamente ligada conduce a la segregación de los roles conyugales. “El grado de segregación en la relación de rol del marido y la esposa varía en relación directa con la connectedness de la red social de la familia” (1957: 60). Tenemos aquí formulaciones que tienen un aire de familia con las diversas solidaridades durkheimianas, o con la grilla y grupo de Mary Douglas, pero que presenta las ideas de manera más tangible y operacional. La “hipótesis de Bott”, como se la conoció durante un tiempo, originó un conjunto de estudios que se sirvieron de ella o intentaron reformularla (Hannerz 1986). Tampoco faltó un aluvión de críticas de las definiciones de Bott, de sus mediciones, su ideología, su muestreo y de la validez general de la hipótesis (Turner 1967; Platt 1969). De lo que no cabe duda es de la productividad de la idea, una idea que estuvo a punto de convertir el concepto de red mismo en una variable independiente, para explicar en función de ella la conducta individual. Casi siempre en la esfera de influencia de la escuela de Manchester, en la antropología social británica tuvieron sus quince minutos de fama “los cinco B-” que realizaron la transición entre el moribundo estructural-funcionalismo de la época colonial y la nueva era de las estrategias accionistas: Barnes, Bott, Barth, Boissevain, Bailey. Barth no fue un teórico de redes de la primera hora, pero en los noventa se volcó hacia esa clase de modelos en nombre de un mayor naturalismo en la conceptualización social (Barth 1992). Entre libros y artículos (y entre Manchester y Harvard), los estudios de redes del período de auge en antropología suman unos trecientos, destacándose aparte de los nombrados los de autores como Geert Banck, el estudioso de la mafia Anton Blok, D. M. Boswell, la estudiosa de género Tessa Cubitt, Arnold L. Epstein [1924-1999], Philip H. Gulliver, Peter Harriet-Jones, David Jacobson, D. G. Jongmans, Nancy Howell Lee, Rudo Niemeijer, Albertus Antonius Trouwborst [1928-2007], Thoden van Velsen, Prudence Wheeldon, Norman Whitten y Alvin Wolfe. Figura 13 – Análisis de embeddeddness en Java, según Schweizer (1997: 747) Aunque durante un tiempo disfrutó de cierto prestigio y ejerció alguna influencia en ese campo desordenado que siempre ha sido el estudio de grupos y la antropología de las sociedades complejas, la carencia de herramientas computacionales, de máquinas comparables a las modernas PCs y de hallazgos dramáticos afectó el desarrollo de este campo de investigación, cuyo último trabajo memorable puede que haya sido la investigación de Bruce Kapferer (1972) sobre el poder y la influencia en una fábrica de Zambia, al filo del crepúsculo de la escuela de Manchester y en los albores del proceso de descolonización. Un cuarto de siglo más tarde las mismas problemáticas fueron abordadas con técnicas de excelencia por Thomas Schweizer en su estudio comparativo entre el intercambio de regalos entre los !Kung y las celebraciones rituales en aldeas javanesas (figura 13); pero ya casi nadie prestaba atención a esas cosas. Ni a los métodos ni a la etnografía, quiero decir. Aún cuando los desarrollos antropológicos claramente se han ganado el respeto de los expertos en redes en general (Wasserman y Faust 1994: 12-13; Scott 2000: cap. 4; De Nooy y otros 2005: xxiii, 98, 226-256, Mika 2007: 29), ya desde el principio sus propios practicantes sabotearon todo viso de sustentación del ARS en antropología. En opinión de Kapferer la noción de red social simplemente designa una técnica de recolección de datos y de análisis; los resultados decepcionantes del análisis pueden atribuirse, decía, a una preocupación indebida por la clasificación y la definición, con muy poca atención a los supuestos teóricos que le subyacen (Kapferer 1973: 167). El propio creador del concepto, John Barnes (1972), afirmaba que no existía tal cosa como una teoría de redes sociales y que quizá nunca llegaría a existir; estaba en ello de acuerdo con Bott, quien pensaba que no había nada revolucionario en dicho método, el cual podía ser utilizado en cualquier marco de referencia (1971: 330): una forma poco sutil de denigrar una de sus mejores virtudes. Ante el hecho de que el concepto de red fue elaborado en forma diferente por distintos autores y de que no todos los que hicieron uso de la idea se sintieron obligados a proporcionar las definiciones precisas que la posicionaran en relación con otras categorías generales, Barnes escribió más tarde:
Desde la perspectiva actual esa actitud autocrítica (asumida en tiempos de la inminente marejada interpretativa) parece algo sobredimensionada y a todas luces inoportuna. Se llegó a decir que la teoría de redes era teoréticamente infructuosa, pues carecía de supuestos básicos de los que se pudiera derivar un conjunto de proposiciones relacionadas entre sí, susceptibles de ser puestas a prueba. Entre los especialistas en ARS de primera línea, Clyde Mitchell fue uno de sus pocos que fue más allá de esas premisas, típicas de un curso sintético de Epistemología 101 como los que entonces plagaban las universidades; él pensaba que lo mismo podía decirse de cualquier otra teoría antropológica; más aún, afirmaba que el hecho de “que se puedan derivar proposiciones a partir de la consideración de las características de las redes sociales es [...] evidente” (Mitchell 1974: 283). Pocos años después de Mitchell, Alvin Wolfe (1978: 53) produciría una profecía fallida, anunciando que si bien el análisis de redes había crecido explosivamente desde 1953, el siguiente cuarto de siglo presenciaría un crecimiento aún mayor. En ocasión de su recensión del texto magno de Wasserman y Faust (1994) sobre ARS, y al tomar nota de quince años de silencio antropológico sobre esa clase de modelos, Wolfe (1997: 219) no tardaría en comprobar que su predicción se había incumplido miserablemente. Aunque se fue de la escena tan discretamente que nunca nadie pudo hablar de un colapso del movimiento ni precisar la fecha de su desaparición, alguna vez (ahora sólo veamos una muestra) habrá que inventariar las razones que se adujeron para explicar el agotamiento de la escuela de Manchester en antropología. Lo primero que salta a la vista es que entre los historiadores no ha habido consenso, quizá porque se buscaron sólo razones endógenas y porque fueron muchas más cosas que el análisis de redes lo que cayó en desgracia en esa época. Escribe Antonio Chiesi, por ejemplo:
El diagnóstico del malogrado Thomas Schweizer, como se ve, no se parece en nada:
Mientras que en sociología se mantuvo el ARS como una especialidad viva que ha adquirido fuerza inédita en los últimos años, ejerciendo influencia en computación y matemáticas (Berkowitz 1982; Mika 2007), en antropología los temas de investigación fueron dejando de lado los temas de estructura y proceso social en beneficio de la función simbólica, la interpretación, la identidad. Para colmo, el especialista Jeremy Boissevain (1979) escribió un estridente artículo en la prestigiosa Current Anthropology que se convirtió en algo así como el obituario de la práctica en la disciplina, el dictamen que dio comienzo a su aislamiento como aplicación de nicho, cuando podría haber sido la práctica sustitutiva del entonces moribundo análisis de parentesco. El declive del análisis de redes en antropología entre (digamos) 1974 y 1995 es una historia tediosa y lamentable que aún no ha encontrado su cronista pero que habrá que resignarse a contar alguna vez (cf. White 2001). Ahora que el ARS ha retornado triunfalmente como una de las manifestaciones de vanguardia entre las disciplinas de la complejidad del nuevo milenio, la antropología no está en su mejor forma para retomar el camino y recuperar el tiempo perdido. Pero lo peor que puede hacerse, creo, es resignarse a dejar que la historia se repita. 8 – Análisis micro, análisis macro y la fuerza de los lazos débilesPocos años atrás, una de las presuntas especialistas en teoría antropológica de la Argentina, manifestó en público que el problema de la relación entre los niveles micro y el plano macro, entre el individuo, la díada, el pequeño grupo y la sociedad, era una cuestión obsoleta, pasada de moda. Más allá de que dicha interpretación no podría jamás sustentarse de cara al estado de las disciplinas y a los datos cuantitativos de referencias cruzadas y temas de investigación que hoy se actualizan casi en tiempo real y que está al alcance de las puntas de los dedos, aquí sostendré que, por el contrario, la naturaleza de las relaciones micro/macro (o local/global, u horizontal/vertical, o incluso sintagmático/paradigmático) sigue constituyendo, cualquiera sea el marco teórico, un problema esencial de las ciencias sociales, antropología inclusive, si es que estas ciencias tienen algún sentido y razón de ser. En consonancia con lo que afirmo, uno de los teóricos sociológicos hoy más reputados, Mark Granovetter, afirmó hacia fines de los años sesenta que una de las debilidades de la teoría sociológica radicaba en su incapacidad para vincular los niveles micro con los niveles macro. ¿Cómo hace, por ejemplo, un actor para operar más allá de su entorno? El análisis de los procesos interpersonales, especulaba, podría proporcionar un vínculo adecuado. Ahora bien, la sociometría, precursora del análisis de redes, siempre ha sido periférica a la teoría sociológica, en parte porque se ha consolidado como perteneciente a la psicología social y en parte porque nunca ha existido una teoría para pasar del plano del pequeño grupo al de las estructuras globales. 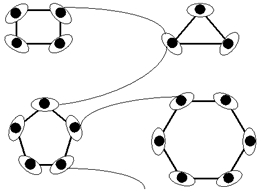Figura 14 – Vínculos fuertes en el interior de grupos, lazos débiles entre los grupos Granovetter, quien todavía era doctorando en Harvard, comienza su trabajo con una definición sumaria pero convenientemente práctica de la fortaleza y la debilidad de los vínculos en una red:
Aunque los trabajos de la escuela antropológica de Manchester habían avanzado en esa dirección, Granovetter encontraba que su tratamiento de las cuestiones estructurales era escueto. Tomando como base algunas ideas del matemático sistémico Anatol Rapoport [1911-2007], uno de los primeros en estudiar la velocidad de propagaciones y la naturaleza de las epidemiologías dentro de las redes, Granovetter examina las características de los lazos que vinculan las díadas, las tríadas y los cliques. Encuentra así que para que se difunda verdaderamente un rumor, éste debe evitar o trascender los nexos fuertes inmediatos y pasar a través de los vínculos débiles. Si se queda en el circuito de los lazos fuertes, sólo alcanzará a unos pocos cliques, pues no se cruzarán los puentes (p. 1366). Los lazos fuertes son los que uno llama amigos; los lazos fuertes, los conocidos [acquaintances]; el conjunto de Ego y de sus conocidos (figura 14) constituye, siguiendo la denominación del antropólogo Arnold Epstein, una red de baja densidad. Tras otros análisis semejantes, Granovetter concluye que la vinculación de los niveles micro y macro no es un lujo teórico del cual se puede prescindir, sino un elemento de extrema importancia para el desarrollo de la teoría sociológica. La teoría urbana de la sociología tradicional (por ejemplo la de Louis Wirth en Chicago) sostenía que los lazos débiles eran generadores de alienación y allí acababa todo; la visión es muy distinta ahora: los lazos fuertes, que alientan la cohesión local, llevan a la fragmentación de la totalidad. Las paradojas, resume Granovetter, son un antídoto deseado para las teorías que lo explican todo demasiado limpiamente (p. 1378). La historia de Granovetter trae a colación un nuevo antipatrón de las ciencias sociales. En efecto, su hallazgo fue rechazado al principio por la prestigiosa American Sociological Review, pues se creyó que violaba el principio de sentido común que establece que los lazos fuertes son los más efectivos en todos los escenarios, porque sí. Con unos pocos retoques que no modificaron ningún argumento clave el artículo fue aceptado finalmente en 1973 por el American Journal of Sociology, convirtiéndose desde entonces (y hasta hoy) en una de las referencias clásicas de la sociología. A partir de allí Granovetter quedó, como se dice en cine, typecasted, encasillado. Cada vez que él (un sociólogo genérico, por otra parte) intenta hablar de sociología, todos esperan que hable de análisis de redes sociales en general y de vínculos reticulares débiles en particular (Granovetter 1990: 13). Y cada vez que los teóricos de redes presentan propuestas innovadoras fuera de su nicho ecológico, lo común es que se encuentren con resistencia. Granovetter (1983) había sugerido que si uno quiere hacer algo importante que se sale de la rutina cotidiana, como por ejemplo conseguir trabajo, más de una vez deberá aventurarse fuera del mundo sobre el cual tiene dominio inmediato. Esta clase de ideas, que en principio surgieron de una corazonada y fueron corroborados mediante unas trecientas encuestas ad hoc en el área de Boston, han sido con los años confirmados por los hechos; estudios independientes, como los de Carol Stack (1974), Larissa Lomnitz (1977) y Eugene Ericksen y William Yancey (1977), probaron que en ambientes urbanos y etnográficos las clases pobres dependen casi exclusivamente de sus lazos fuertes, una idea sugestiva que en modo alguno explica la pobreza pero que constituye al menos una buena hipótesis de trabajo a propósito de sus posibles consecuencias. El propio Granovetter refinó el concepto de lazos débiles con los años. Basándose en datos cuantitativos precisos de los ya nombrados Ericksen y Yancey que consideraban también variables de educación, Granovetter halló que en los niveles más bajos de la escala social el uso de lazos débiles para la promoción laboral, contrariamente a las predicciones primarias de la hipótesis, poseían un impacto negativo, pero que ese impacto se iba atenuando a medida que el nivel de educación ascendía. El método utilizado en el estudio empírico original fue un simple análisis de regresión. Nan Lin, Walter Ensel y John Vaughn (1981), en cambio, usaron métodos similares a los promovidos por el metodólogo Peter Blau [1918-2002], consistentes en modelos de ecuaciones estructurales y path analysis para medir la contribución relativa de distintas variables independientes a alguna clase de variable dependiente, en este caso el status ocupacional. Su hallazgo ha sido también esclarecedor: el uso de lazos débiles para encontrar trabajo posee una alta asociación con un logro laboral más alto sólo si los lazos débiles conectan al candidato con gente mejor ubicada en la estructura ocupacional. Todos estos estudios y una docena más que no he de tratar aquí clarifican las circunstancias bajo las cuales los lazos débiles proporcionan un valor agregado: sólo los lazos débiles que forman puente son de especial valor para los individuos; la ventaja de los lazos débiles es que es más probable que éstos sean puentes y no los lazos fuertes u homofílicos. Contrástese este principio con el que afirma que el coeficiente intelectual, variable de una raza a la otra, es un buen predictor de los resultados que uno obtenga en la vida, como por ejemplo los ingresos o el estatus social (Pinker 2003: 227). Aunque no puedo hablar en nombre de la comunidad de los teóricos de redes, en primera instancia parece más plausible la idea de que las clases pobres o determinados grupos raciales tienen más o menos éxito en la promoción social debido a las constituciones diferenciales de las redes que integran y a las capacidades concomitantes de éstas, y no a causa de la forma en que está biológicamente distribuida la inteligencia entre los individuos que conforman los grupos. El estatuto y la fuerza de la teoría de redes en sociología se debe a muchos factores, pero la centralidad de la figura de Granovetter pudo haber tenido algún impacto al menos en ciertos amplios sectores de la disciplina. De ningún modo es un sociólogo marginal. Las enciclopedias sociológicas recientes lo consideran sin ambages como el fundador mismo de la sociología económica, que se origina en ese mismo documento canónico sobre el embebimiento de la economía en la sociedad y la cultura; en ciencias económicas es uno de los referentes de la econofísica (Swedberg 1990: 96-114; 2000: 734-736). Los especialistas en antropología económica deberían conocer al menos de nombre este campo de estudio en crecimiento dinámico, en el que la teoría de redes configura la forma normal de investigación. Junto a la teoría de los lazos débiles, los antropólogos han desarrollado otros métodos bien conocidos para analizar dinámicas sociales y comparar usos a través de las culturas; el más notorio gira en torno del concepto de embeddedness (Schweizer 1997), al cual, por razones del espacio argumentativo requerido para hacerle justicia, no podré tratar con el detenimiento debido. Tras haber sido acuñado por Karl Polanyi [1886-1964] en la década de 194012, el significado actual del concepto se remonta por lo menos a trabajos de Mark Granovetter (1985) sobre la acción económica y la estructura social; en su faceta “vertical” denota la duplicidad de las vinculaciones jerárquicas de actores a nivel local con la sociedad, la política y la economía de la que forman parte; en la perspectiva “horizontal”, comprende la interpenetración de los dominios sociales y culturales, materiales e ideológicos: toda interacción económica está embebida en relaciones sociales; ésa es la idea, susceptible ahora de representarse y modelarse con palpable solidez. Tal como lo intuyó el lamentado antropólogo Thomas Schweizer [1949-1999] en sus últimos años, la elaboración de esas relaciones categoriales basadas en redes ilumina tanto las viejas polémicas de la antropología económica sustantivista como las nuevas estrategias de George Marcus referidas a la etnografía multisituada (cf. Reynoso 2008; Isaac 2005: 15; Laville 2007). Consecuencia n° 6: El puente entre lo micro y lo macro no sólo es una posibilidad conceptual, sino que constituye un ingrediente clave de la experiencia cotidiana. Es justo decir que aunque un número enorme de investigaciones abonan estas hipótesis todavía no hay una demostración exhaustiva, concluyente y axiomática. Pero en primer lugar este conjunto de hallazgos justifican poner en tela de juicio la falta de resultados impactantes como una tacha histórica de los estudios de redes; no sólo hay resultados de fuste, sino que ellos se ofrecen en campo en el que los antropólogos sólo pueden aportar buenas intenciones. Y en segundo lugar, esta experiencia epistemológica nos demuestra que deberíamos superar la clausura operativa a que nos condena el sentido común, el cual siempre tiende a imponer la idea de que lo mejor es lo más grande, lo más fuerte, lo más conocido. 9 – El advenimiento de los Mundos PequeñosEntre otras propiedades interesantes, las redes ER son modelos aceptables de pequeños mundos, por razones matemáticamente inevitables pero empíricamente irreales. Si alguien tiene cien o mil conocidos (un número realista) y cada uno de éstos tiene otros tantos, cualquier miembro de la población humana estará entre unos ocho y unos diez pasos de distancia geodésica de cualquier otro. Esta es la esencia de la idea de los mundos pequeños. Igual que sucedió con el “efecto mariposa”, entrevisto por Ray Bradbury en A sound of thunder (1952) algunos años antes que se lo redescubriera en dinámica no lineal bajo la categoría apenas más austera de “sensitividad extrema a las condiciones iniciales”, la idea de pequeños mundos se pensó antes en literatura que en ciencia. En 1929 el escritor húngaro Frigyes Karinthy [1887-1938] publicó una colección de cuentos titulada Minden masképpen van (“Todo es diferente”) que incluye uno titulado Láncszemek (“Cadenas”). Se rumorea que el relato (que no he leído) no es nada del otro mundo, pero incluye este asombroso momento:
El episodio anticipa exactamente la clase de concepto que años más tarde habría de hacerse popular como “los seis grados de separación”. El estudioso que engendró esta idea no es otro que el psicólogo Stanley Milgram [1933-1984], el mismo que diseñara un famoso experimento que comprobó lo fácil que es inducir a un ciudadano común, políticamente correcto, a que aplique castigos lindantes con la tortura por razones baladíes. 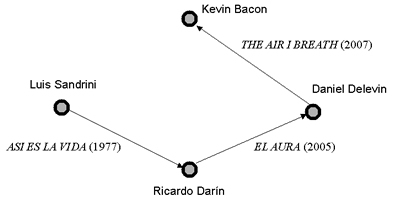Figura 15 – Los grados de separación de Kevin Bacon La segunda gran idea de Milgram (1967) es menos horrorosa pero no es menos sorprendente. Iniciando una cadena de cartas que tenían por destinatario final a una persona escogida más o menos al azar en Boston, Massachusetts, Milgram envió cartas a residentes también aleatorios de Omaha, Nebraska, en el otro extremo de la escala social. En las cartas les pedía a éstos que si conocían al destinatario, que le enviaran la carta directamente; si no lo conocían, que se las remitieran a otra persona de su conocimiento que pudiera tener alguna probabilidad de conocerlos. En cuanto a los resultados, se dice que cierto número de cartas (64 de 217) llegaron a destino; algunas de las cadenas requirieron 12 pasos, pero el promedio de pasos fue de sólo 5.2 (Travers y Milgram 1969: 431). Redondeando magnánimamente hacia arriba, de allí viene lo de los seis grados de separación, aunque Milgram mismo jamás utilizó esta frase. Quien lo hizo por primera vez fue John Guare, en la obra de teatro de 1991 Six degrees of separation, luego transformada en una película en la que el personaje a cargo de la actriz Stockard Channing desarrolla un razonamiento similar al que se encuentra en el relato de Karinthy. Lo que descubrió Milgram (y lo que había intuido antes el escritor) es que la longitud de camino característica de un red es órdenes de magnitud menor que la dimensión reticular. Milgram documentó este hallazgo impresionante en un artículo breve de una revista popular, Psychology Today (Milgram 1967) y algo más tarde en un artículo más detallado en coautoría con Jeffrey Travers en Sociometry. Contemporáneamente a este último, Milgram hizo otro junto con Charles Korte introduciendo gente de diferente raza a lo largo de la cadena sin que los resultados variaran sensiblemente. En rigor los estudios y los descubrimientos de Milgram habían sido precedidos por un artículo de Manfred Kochen e Ithiel de Sola Pool (1978) de mediados de los cincuenta (citado por Milgram como un inédito) que demoró casi veinte años en publicarse. 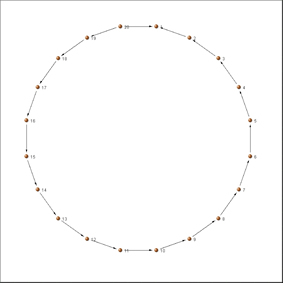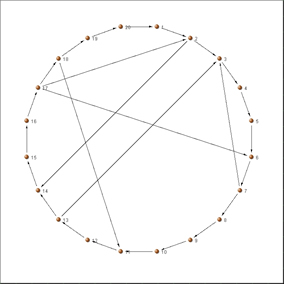Figura 16 – Grilla regular y grilla regular SW re-cableada El producto más conocido derivado de esta idea es el Oráculo de Kevin Bacon en la Universidad de Virginia, donde se puede proponer el nombre de (casi) cualquier actor o actriz y verificar su distancia geodésica (o sus grados de separación) de aquel actor en particular (véase http://oracleofbacon.org). Los comportamientos notables de esta red de algunos millones de nodos ocurren a nivel de agregado, pues sucede que Bacon (junto a otros mil o dos mil actores) está a muy pocos grados distancia de cualquier otro actor. La imagen de la figura 15 muestra que, por ejemplo, la red de pequeños mundos desde el improbable Luis Sandrini hasta Kevin Bacon. Contra todo pronóstico, Sandrini se encuentra sólo a tres grados de separación, o sea que tiene un “número de Bacon” igual a 3. ¿Un tío influyente? No; las redes son así, y a cualquiera le puede pasar. A todos, de hecho, hasta que algún teorema demuestre lo contrario. Como suele suceder, tanto el experimento de Milgram como la idea misma de los seis grados fueron puestos recientemente en tela de juicio; Judith Keinfeld (2002), en particular, procuró degradarlos como si fueran sólo mitos urbanos, aduciendo irregularidades y lagunas de documentación en la ejecución del experimento original. Diversas experiencias con toda clase de redes, empero, confirmaron que las redes grandes, y en particular las que veremos seguidamente, poseen en efecto la propiedad de pequeños mundos, algunas de ellas en el mismo orden de magnitud que el mito urbano, otras incluso por debajo. Los modelos de pequeños mundos comenzaron a ser tratados a partir de las elaboraciones de Duncan Watts y Steven Strogatz en la década de 1990. Ellos proponen tomar como punto de partida una grilla regular parcialmente “re-cableada”; en el camino comprobaron que si a una grilla regular como la de la izquierda de la figura 16 se le añaden unos poquísimos vínculos al azar, la conectividad de esa red aumenta (o su diámetro disminuye) en un número que se diría es absolutamente desproporcionado, con absoluta independencia del tamaño de la red. La red de la derecha, por ejemplo, diseñada con Agna 2.1, presenta una estadísticas de betweenness, distancia geodésica, diámetro y demás radicalmente diferente de las del caso de la izquierda. Si se agregan algunos cientos de nodos el efecto no varía mucho. Nada en todo este campo es proporcional a ninguna otra cosa. Cuando se tratan de razonar las explicaciones del caso, se descubre que en la estructura de las redes al azar hay algo importante que está fallando. Si bien estas redes son modelos más aceptables de los mundos pequeños que las grillas regulares, no dan cuenta de una propiedad esencial de las redes en la vida real: los amigos de los amigos de uno tienden a ser amigos entre sí; esta es la propiedad de clustering, que en una red aleatoriamente estructurada no sólo es improbable sino taxativamente imposible. En efecto, en un grafo al azar la probabilidad de que dos amigos de A sean amigos entre sí no es mayor que la que tienen de ser amigos dos personas cualesquiera de la población mundial, estatal o lo que fuere. Consecuencia n° 7: La primera lección a sacar aquí, epistemológicamente hablando, es que el azar es un pobre modelo de las estructuras de red que se encuentran en la vida real; más todavía, lejos de constituir una heurística útil, el azar es en estos escenarios un modelo inhibidor que impide abordar y comprender estructuraciones esenciales de la realidad. Consecuencia n° 8: La siguiente lección, no menos importante, consiste en haber aprendido que en los sistemas regidos por la complejidad las propiedades no son siempre proporcionales al número de los elementos que lo componen. En dinámica no lineal los sistemas llamados caóticos son casi siempre de muy baja dimensionalidad, sumando típicamente dos o tres entre variables y parámetros. En estos sistemas existen ciertos comportamientos que no resultan más complejos si el número de elementos es más grande o si se introduce aleatoriedad (Reynoso 2006). 10 – Encuentro de las redes y la complejidad: Redes libres de escalaEn todo el siglo XIX y en los primeros años del siglo XX las redes se consideraban a veces como si fueran regulares y otras como si fueran euclideanas en aras de la simplicidad; más tarde, en cuatro de las últimas cinco décadas, la ciencia trató la mayor parte de las redes empíricas, siguiendo a Erdös y Rényi, como si fueran aleatorias. Podrá decirse que fue un mal necesario; la simplicidad de esta estrategia hizo que floreciera la teoría de grafos y que surgiera una rama de las matemáticas especializada en redes aleatorias. Las redes ER son exponenciales: tienen un pico en un valor promedio y su caída es abrupta. Como ya se ha visto, en este modelo todos los nodos tienen aproximadamente la misma cantidad de vínculos, lo que resulta en una distribución de Poisson en forma de campana, como se muestra en la figura 17 (b). En 1998 Albert-László Barabási, Eric Bonabeau, Hawoong Jeong y Réka Albert se embarcaron en un proyecto para trazar el mapa de la Web, pensando que iban a encontrar una red aleatoria. Las mediciones, empero, refutaron esa expectativa: la totalidad de la Web se sustentaba en unas pocas páginas altamente conectadas, que en el modelo se identificaron como hubs; la gran mayoría de los nodos, comprendiendo más del 80% de las páginas, tenía poquísimos vínculos, menos de cuatro. Entre ambos extremos estaban representadas todas las frecuencias posibles, o casi. Contando el número de páginas que tienen exactamente k vínculos, resultó evidente que la distribución seguía un patrón de ley de potencia: la probabilidad de que un nodo estuviera conectado a k otros nodos era proporcional a 1/kn. Cuando hay una distribución de ley de potencia, hay también independencia de escala, como después se verá: no hay una medida típica, ni hay valores promedios que describan el conjunto; para la estadística tradicional, esos sistemas son casi intratables. Por añadidura, las redes LE obedecen leyes de escala que son características de los sistemas que se auto-organizan. 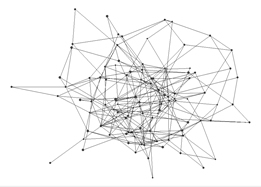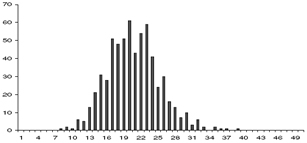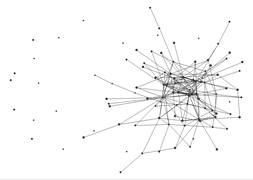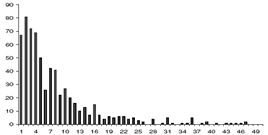Figura 17 – Red aleatoria (a, b) y red independiente de escala (c, d) Era indudable que se había descubierto una nueva clase de red, menos “teórica” y mucho más conspicua en la vida real que la de Erdös y Rényi. La expresión “redes libres de escala” (scale-free networks) fue acuñada por Barabási para referirse a ella. El centro neurálgico de las investigaciones en redes LE es la Universidad de Notre Dame en Indiana, donde Barabási dirige un activo grupo de investigación, el cual participa en el desarrollo del programa Network Workbench. Tras la primera comprobación, comenzó a hacerse evidente que las redes de este tipo aparecían en los contextos lógicos y materiales más disímiles: relaciones sexuales, agendas telefónicas, nexos sintácticos entre palabras en un texto o discurso, citas bibliográficas entre miembros de la comunidad académica, colaboraciones en reportes de investigación, alianzas tecnológicas, relaciones entre actores de cine, sinapsis neuronales, contactos entre personas en una organización, cadenas alimentarias, conexiones entre organismos vinculados al metabolismo o proteínas reguladoras, propagación de enfermedades y virus informáticos (Barabási y Bonabeau 2003; Liljeros y otros 2003). Los investigadores de Notre Dame y otros que se unieron al estudio descubrieron en esta clase de redes LE un número inesperado de propiedades. Tienen, por empezar, una extraordinaria robustez: se puede destruir el 80% de los nodos que el resto seguirá funcionando. Pero también son desproporcionadamente vulnerables a ataques selectivos: una eliminación del 5 al 10% de los hubs, que son poquísimos en relación al tamaño de la red, alcanzaría para hacer colapsar al sistema o quebrar su unidad. Artículos aparecidos en el momento de explosión de estos hallazgos en Nature y en Science promovían afirmaciones aún más extremas: “Internet es robusta pero frágil. El 95% de los vínculos se pueden remover y el grafo seguirá conectado. Sin embargo, la eliminación planeada de 2,3% de los hubs desconectaría la Internet”. Aunque esas evaluaciones se saben hoy exageradas13, el modelo LE no sólo sigue en pie sino que permite conciliar el hecho que muchas redes reales presentan conglomerados o clusters jerárquicos, un factor que el modelo aleatorio ER no es capaz de tratar. Se sabe además por simple observación que las redes LE surgen cuando a una red existente se van agregando nuevos nodos, y que éstos prefieren ligarse a otros que están bien vinculados. Esta vinculación selectiva se llama efecto de “el rico se vuelve más rico”, o principio de San Mateo, bautizado así por el sociólogo Robert Merton muchos años atrás (Barabási 2003: 79-92; Wang y Chen 2003: 14; Watts 2004: 108, 112). Examinando el sostema científico de recompensas, Merton observó que los científicos eminentes obtienen un crédito desproporcionado por sus contribuciones, mientras que los que son relativamente desconocidos obtienen muchísimo menos por contribuciones comparables. La recompensa cae, en general, en manos de quienes ya son famosos. La referencia a San Mateo, proporcionada sin mención de capítulo y versículo es la que dice que “Al que ya tiene le será dado, y tendrá en abundancia; pero al que no tiene incluso lo que tiene le será quitado” (Merton 1968: 68; Mateo 13 §12). Entre paréntesis, señalo que la metodología de Merton en ese ensayo se basa en un anecdotario impresionista y nada tiene que ver formalmente con análisis de redes o modelos matemáticos. Antes se creía (Fritjof Capra todavía lo cree) que las redes que se auto-organizaban sin necesidad de un gobierno o jerarquía vertical eran democráticas y benevolentes; ahora se sabe que no es así. Como sucede a menudo en estas ciencias, los matemáticos tomaron gustosos la vieja metáfora de la sociología que describe un escenario en el cual, aunque las elecciones individuales son impredecibles, como grupo todo el mundo sigue estrictamente unos pocos patrones. Aunque nuestro antropólogo basaba sus conclusiones correctas en las premisas equivocadas, esto constituye una verificación colateral de una vieja idea de Gregory Bateson (1980: 36-40): las secuencias divergentes, los aspectos singulares de un sistema complejo son impredecibles; los aspectos convergentes o universales son siempre los mismos y por ende se pueden predecir. La calidad y relevancia de las secuencias que se propongan dependen de la imaginación del científico, no habiendo ninguna marca formal que determine que las divergentes son por necesidad las más sagaces, las más humanas o las más realistas. Contradiciendo a Clifford Geertz (2000: 135), no necesariamente los universales de las ciencias blandas conciernen a ideas consabidas o triviales. Una vez caracterizadas las propiedades de las redes LE y descubiertas en manifestaciones de distinta materialidad, los descubrimientos y los lineamientos para operar en esta clase de redes en ciencias sociales (antropología inclusive) sobrevinieron en tropel. Otras propiedades de las redes LE vuelven a desafíar el sentido común: por razones que aún se siguen discutiendo, el valor de n en el término kn de la ley de potencia tiende a caer siempre entre 2 y 3; dada la estructura de estas redes, además, cualquier nodo está conectado con cualquier otro con muy pocos grados de separación, alrededor de seis cuando los nodos son unos cuantos cientos de miles, no más de diecinueve entre cualesquiera de los cuatro mil millones de páginas de la Web. Por otra parte, en una red LE es posible encontrar nodos cuyo valor de conectividad supera varias veces el número promedio, lo que no es propio de las distribuciones aleatorias, como la que rige la tabla de estaturas de una población, donde nunca se encontrará una persona que sea mil o un millón de veces más alta que otra. Dada la distribución peculiar de estas redes, muchas de las técnicas estadísticas, incluso muchas de las que vienen incluidas en los programas de redes (muestreo, análisis de varianza, generalización, coeficientes de correlación) son inadecuadas para lidiar con ellas, puesto que presumen distribuciones normales, linealidad y regímenes estables; esto es algo que las ciencias sociales han estado ignorando hasta ahora. Y cuando digo ahora intento significar exactamente eso: hasta los últimos dos o tres años del siglo XX, para ser preciso. En estas redes LE también es irregular el comportamiento dinámico. Las teorías clásicas de la difusión, que se desarrollaron durante décadas en estudios de mercadeo y epidemiología, predicen un umbral crítico de conectividad para la propagación de un contagio, rumor o novedad a través de una población. Para que un virus, una noticia, un motín o lo que fuere se difunda, debe superar ese umbral; de otro modo terminará extinguiéndose. Pues bien, hace poco se demostró que en las redes LE el umbral es cero, lo cual implica que cualquier elemento contagioso encontrará la forma de dispersarse y persistir en el sistema, por más que su capacidad de contagio sea débil (y sobre todo si lo es, según dicen). Esto tiene consecuencias drásticas para el planeamiento de campañas de vacunación, distribución de ayuda humanitaria en situaciones de emergencia, tácticas de insurgencia o contrainsurgencia u otros escenarios por poco que se sepa uno manejar con estas redes de manera adecuada: tomar como blanco unos pocos hubs más conectados es mucho más efectivo y económico que aplicar la solución a un porcentaje enorme de nodos. Inmunizando los hubs, por ejemplo, podría impedir que se propague una epidemia. Otros objetivos y efectos los dejo librados a la imaginación. Además del efecto de los pequeños mundos, del umbral de percolación y de la robustez, cada investigación sistemática que se lleva a cabo descubre comportamientos impensados que obligan a reformular las hipótesis de trabajo o a quebrar mitos hace tiempo instalados en la comunidad. Una idea central del marketing y de la investigación sobre procesos de difusión, por ejemplo, ha sido que los influenciadores son importantes en la formación de la opinión pública. Esa idea fue popularizada por Paul Lazarsfeld, Elihu Katz y sus colegas en el famoso modelo del “flujo de los dos pasos” que introducía formadores de opinión entre la influencia mediática y la población en general, suplantando al siempre dudoso modelo hipodérmico. La investigación reciente ha demostrado que, por el contrario, las avalanchas de cambio en la opinión dependen menos de influenciadores poderosos de que cierta masa crítica mínima de individuos fácilmente influenciables, que a su vez impactan sobre otros de su misma condición. En algunos escenarios, ciertamente, los formadores de opinión son responsable de dramáticos efectos de cascada; pero los modelos matemáticos recientes parecen comprobar que esas instancias son más la excepción que la regla: en la mayor parte de los casos, los influenciadores son sólo un poco más importantes que los individuos comunes (Watts y Dodds 2007). Dado que algunas redes son aleatorias (la red eléctrica o las carreteras de un país), otras en apariencia análogas son LE (la red de aeropuertos, Internet) y otras más son mixtas o irregulares, el investigador deberá encontrar de qué clase de red se trata usando el ya familiar gráfico log-log: si la red es LE, el logaritmo del número de nodos contra el logaritmo del número de vínculos resultará en una línea recta (figuras 17-d y 19). La inclinación de esa línea mide la dimensión fractal y, según afirman muchos, la complejidad del sistema. La “cola” de una distribución de este tipo tiene una caída mucho más suave que la de una distribución en forma de campana, lo que quiere decir que hay en ellas mayor diversidad. Las matemáticas de las redes LE son además muy simples y sus usos parecen ser innumerables; su marco teórico se vincula con problemáticas de auto-organización, criticalidad, percolación y hasta fractales. 11 – Ley de potencia: Los significados de una distribuciónTenemos entonces que la distribución del valor que fuere en el seno de las redes LE no es aleatoria. Matemáticamente, aunque simplificando un poco, la distribución propia de estas redes es lo que se denomina distribución 1/f o de ley de potencia (power law). Esta distribución está entre las leyes más frecuentes que describen la invariancia de escala en muchos fenómenos materialmente disímiles. Dando un giro a lo que antes dije, la invariancia de escala se encuentra asimismo vinculada a la autosimilitud y la auto-organización, y es un rasgo característico de las transiciones de fase en las proximidades de un punto crítico. Una relación de ley de potencia entre dos magnitudes escalares x e y es una relación que se puede escribir de este modo y = axk donde a (la constante de proporcionalidad) y k (el exponente de la ley de potencia) son constantes. Puede decirse que este exponente es la característica principal de la distribución, pues describe de qué manera cambia ésta como función de la variable subyacente. Por ejemplo, si el número de ciudades de cierto tamaño decrece en proporción inversa a su tamaño, el exponente es 1. Si decrece inversamente al cuadrado el exponente es 2, y así sucesivamente. Hay diversas formas de escribir la misma relación, más o menos interpretadas o expresivas. Una modalidad común es ésta: P = cM-α Donde P es la probabilidad, c una constante, M una medida y α un exponente de escala. En esta interpretación, este exponente es llamado exponente de Hurst o dimensión fractal cuando la distribución se observa en el tiempo o en el espacio, respectivamente (Csermely 2006: 325). Un exponente de Hurst (H) o índice de dependencia, nacido en hidrología para calcular el tamaño de las represas para el Nilo, varía entre cero y uno; un valor mayor significa una trayectoria más suave, menos volatilidad y menor rugosidad. La dimensión fractal puede calcularse como D = 2 – H. A partir de lo que hemos visto hasta aquí, es posible ahora identificar numerosas relaciones de ley de potencia, tales como la ley de Stefan Boltzmann (la energía irradiada por un cuerpo oscuro es proporcional a la cuarta potencia de su temperatura termodinámica), la ley de mortalidad de Benjamin Gompertz que se usa para cálculo de seguros desde 1825, la ley de Max Kleiber que vincula el metabolismo de un animal con su tamaño y hasta la ley de Newton, en la cual la fuerza gravitacional resulta ser inversamente proporcional al cuadrado de la distancia entre dos cuerpos. El antropólogo Gregory Bateson demostró tener alguna intuición de estas ideas en el extraño episodio del caballo poliploide de su libro Espíritu y naturaleza (Bateson 1980: 49-53). 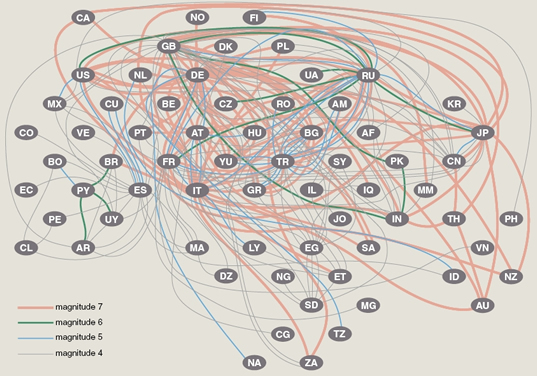Figura 18 – Red de conflictos internacionales Es importante tener en cuenta que la invariancia de escala no es una categoría nacida en las ciencias duras o abstractas, sino que fue descubierta y acuñada por el meteorólogo Lewis Fry Richardson [1881-1953] al examinar la frecuencia de los conflictos grandes y pequeños (desde las guerras mundiales hasta los asesinatos domésticos) como una función de su severidad, medida en número de víctimas fatales directas (Richardson 1948). En un campo que parecían haber agotado figuras mayores como Pitirim Sorokin y Quincy Wright, Richardson formuló ideas sobre la escalada de la carrera de armamentos que influyeron en la noción de esquismogénesis de Bateson y llegó a algunas otras conclusiones sorprendentes. La figura 18 muestra la red de las guerras de magnitud superior a 3.5 en la escala de Richardson; una escala logarítmica, no necesito decirlo, de base 10 en este caso: una campaña de terror que mata a cien tiene una magnitud de 2, una guerra en que muere un millón una magnitud de 6; alcanza con contar los ceros. La denominación de los países sigue la nomenclatura de la Web. Argentina aparece abajo a la izquierda con sus guerras contra Uruguay, Brasil, Francia, España, Gran Bretaña y, a otra escala, Paraguay (basado en Hayes 2002: 14). En el estudio de Richardson, el número de países o imperios considerados rondaba los sesenta. El número promedio de países fronterizos, con los que la probabilidad de conflicto era más alta, era seis; Richardson, basado en un elegante argumento geométrico inspirado en la relación euleriana entre los vértices, las aristas y las caras de un poliedro, demostró además que debían ser aproximadamente seis para cualquier disposición geográfica de naciones. Existía entonces una probabilidad de 10% de que cualquier par de beligerantes fueran países fronterizos. En fin, no viene el caso resumir el conjunto del ensayo, continuado en la actualidad con mejores recursos por autores como David Singer o Peter Breke. Si bien Richardson nunca dibujó un grafo (como tampoco lo hizo Euler), prefiguró un fragmento importante de la teoría de redes hasta en los más precisos detalles algorítmicos. La figura 19 muestra otro hallazgo colosal de Richardson, que es el que compete a la dimensión fractal de diversas curvas fronterizas, en contraste con la de un círculo. A medida que disminuye la unidad de medida, aumenta la longitud de la medición; las costas de pendiente más empinada (es decir, las de mayor dimensión fractal) son las más accidentadas; el círculo la longitud total tiende rápidamente un límite apenas comienza a disminuir la unidad de medida (Mandelbrot 1967). 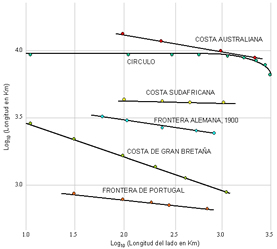Figura 19 – Dimensión fractal de las costas (Richardson 1961: fig. 17) Entre paréntesis, me interesa señalar algunos otros hallazgos convergentes que se encuentran en el estudio de Richardson en los términos en que lo ha elaborado Brian Hayes, imposibles de superar:
El lector podrá reconocer en esta instancia digna de Nelson Goodman la raíz y la clave de no sólo la geometría fractal y de su concepto de dimensiones fraccionales, sino un episodio que revela, como en toda ciencia interesante, las fuerzas que se desatan cuando se formula la pregunta crítica en el escenario oportuno: ¿Cuánto mide la costa de Gran Bretaña? fue aquí la cuestión canónica, el modo de esconder recatadamente, detrás de un asunto particular, que se estaba aportando un elemento de juicio esencial a lo que luego sería el más universal de todos los campos del saber (Mandelbrot 1967). Las mismas técnicas de cálculo basadas en ecuaciones diferenciales, de hecho, le sirvieron a Richardson para estudiar los fenómenos meteorológicos, la psicología, las turbulencias, la dimensionalidad de las curvas costeras y los conflictos armados. Al lado de las que puso de manifiesto Richardson hay infinidad de leyes de potencia adicionales escondidas en la investigación sociocultural. Inspirándose lejanamente en la “ley de gravitación social” de Émile Durkheim, hace poco se ha resucitado la teoría de interacción espacial de William Reilly (1931), que trasplantaba la ley de Newton al campo de las interrelaciones entre locaciones y transporte en la adquisición de mercaderías por parte del consumidor (“ley de gravitación de la compra al menudeo”). Años más tarde Alan Wilson (1967, 1970, 1974) verificó esta temprana intuición, que hoy es un lugar común en los modelos de interacción espacial en planeamiento y estudio urbano (Bertuglia y Vaio 2005: 214-230). Muy poco de esto se ha filtrado a los jornaleros de la estadística o del análisis de redes, y sobre lo poco que se filtró algunos han erigido mitologías. Como sea, la distribución de ley de potencia aparece también en la investigación social cuando uno se pregunta cuánta gente hay que tiene qué cantidad de dinero (ley de Pareto), en lingüística cuando se analiza la distribución de las palabras en un texto (ley de Zipf), en criticalidad auto-organizada y en sismología (ley de Gutenberg-Richter), en la música estéticamente “aceptable” (distribución 1/f o ruido rosa), en el comportamiento dinámico de los públicos musicales (cuánta gente escucha qué géneros) y en la vida de los géneros estilísticos (Voss y Clarke 1975; Bak 1996). Según Baumann y Stiller (2005: 348) en redes complejas la ley de potencia se manifiesta no sólo en la distribución de grados sino en otras propiedades del grafo:
Vale la pena aclarar este último punto, por cuanto permite establecer otras correspondencias con otros dominios complejos del conocimiento. En análisis de redes uno se encuentra constantemente con conceptos tales como eigenvalores o eigevectores (o sus equivalentes en castellano como autovalores y autovectores) que en este campo se dan por consabidos pero al que muy pocos antropólogos han demostrado conocer. No voy a explicar aquí de qué se trata esto en profundidad, pero sí voy a señalar algunos indicios importantes. El lector puede encontrar una definición excelente de eigenvectores, eigenvalores y eigenespacios, así como una introducción perfecta al álgebra lineal y a las transformaciones lineales del espacio) en el artículo “Vector propio y valor propio” de Wikipedia (accesado en marzo de 2008); de allí se puede pasar a literatura más completa y exigente14. Un vector (que usualmente es representado mediante una flecha) posee una longitud (que se llama magnitud) y una dirección. Una transformación lineal opera sobre un vector para modificar ya sea su magnitud o su dirección. Un eigenvector de una transformación lineal es un vector que se multiplica por una constante, llamada eigenvalor. La dirección de un eigenvalor o bien se mantiene para eigenvalores positivos, o bien se invierte para los negativos. En el ejemplo del tatuaje maorí que uso habitualmente como símbolo de una imagen compleja el dibujo se ha deformado de tal manera que el eje vertical (el vector rojo) no se modificó pero el azul sí, puesto que cambió de dirección (figura 20). Por lo tanto el vector rojo es el eigenvector de la transformación y el azul no lo es. Dado que el vector rojo no se ha estirado ni comprimido su eigenvalor es 1. Todos los vectores en esa misma dirección son también eigenvectores. Junto con el vector cero conforman el espacio propio para ese eigenvalor. 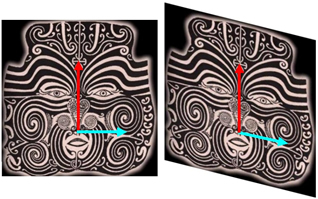Figura 20 – Eigenvector (rojo) En teoría de redes, el vector propio de un grafo se usa para medir la centralidad de sus vértices. El valor propio de un grafo es el eigenvalor de la matriz de adyacencia de un grafo. Estos elementos se usan, por ejemplo, en los algoritmos PageRank de Google (basado en el Science Citation Index) utilizados para asignar relevancia a las páginas en el motor de búsqueda. El análisis de los vectores matriciales correspondientes a un grafo se denomina análisis espectral. 12 – Las redes complejas del lenguaje y el textoEl ejemplo más dramático que permite visualizar y comprender las distribuciones de ley de potencia probablemente sea el de los nuevos estudios en lingüística estadística, que a partir de comienzos del siglo actual constituyen uno de los puntales que han revivido, siempre en términos de redes, el campo de las teorías de sistemas complejos. El siguiente caso proviene de un paper de Ricard Solé, Bernat Corominas Murtra, Sergi Valverde y Luc Steels (2005), especialistas de la Universitat Pompeu Fabra, el SFI, Sony de París y la Vrije Universiteit de Bruselas, respectivamente. Tomando como modelo una muestra de texto, aquí el comienzo de A room of one’s own de Virginia Woolf (A), se definen diferentes tipos de relaciones entre palabras (B), que aquí son relaciones de precedencia (flechas en azul) y relaciones sintácticas (flechas en negro). Los vínculos de la red ilustrada en (C) denotan la red de co-ocurrencia, o sea el universo potencial de frases que se pueden construir con el léxico que constituye el corpus. Un ejemplo de tales caminos es la frase indicada en rojo, “I will try to explain”. Los nodos están coloreados proporcionalmente a su grado, con el color más claro para las palabras mejor conectadas. 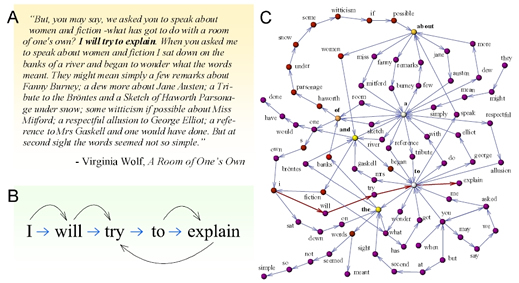Figura 21 – Distribución libre de escala en texto (1) La red representada en (D) es la red sintáctica, tomando como marco descriptivo la dependencia sintáctica de acuerdo con la gramática de dependencia de Igor Mel’čuk (1985; 2003), quien ya tenía un modelo reticular en los ochentas; en este procedimiento, se toma como criterio que los arcos comiencen en complementos y finalicen en el núcleo de la frase, que en frases bien formadas ha de ser el verbo. La frase del ejemplo anterior aparece allí disecada en dos caminos diferentes que convergen en “try”. Tanto (C) como (D) muestran con claridad una estructura de mundo pequeño y una distribución de ley de potencia, que puede apreciarse todavía más rotundamente en el grafo (E), que ilustra la red de co-ocurrencia de un fragmento de Moby Dick.
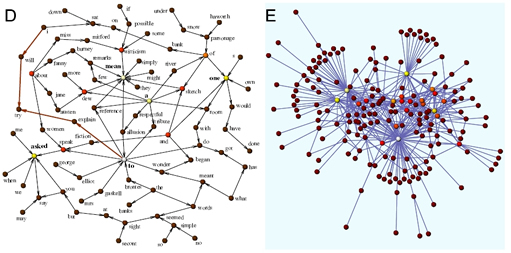
Figura 22 – Distribución libre de escala en texto (2) Otros miembros del mismo equipo de investigación, Bernat Corominas-Murtra, Sergi Valverde y Ricard Solé (2007) han publicado otros descubrimientos notables referido a las transiciones abruptas que se manifiestan en la adquisición del lenguaje desde la etapa de balbuceo hasta el dominio de una forma de expresión similar a la de los adultos. Como se muestra en la figura 22, después de un período susceptible de modelarse con grafos de dependencia muy simples de dos o tres elementos, a los 25 meses se pasa a una etapa que puede representarse con grafos en árbol, en la cual elementos semánticamente degenerados como “there” o “it” actúan como hubs. En esta etapa todavía faltan muchas palabras esenciales en la sintaxis adulta (a, b). Finalmente, en la transición abrupta definitiva (c) los hubs pasan de ser elementos degenerados a ser elementos funcionales, como “a” o “the”, y la red es más densa, rica, con estructura de pequeños mundos y resueltamente libre de escala. Los estudios reticulares del lenguaje, que no existían siquiera a fines del siglo pasado, dieron un paso adelante con las investigaciones de Adolfo Masucci y Geoff Rodgers (2006), quienes refinaron los modelos españoles descubriendo diversas distribuciones libres de escala en el lenguaje escrito, como si existieran diversas clases funcionales de vértices. Hasta la fecha el modelo preferencial de dinámica en estudios de la naturaleza LE del lenguaje sigue siendo el de Sergey Dorogovtsev y José Fernando Ferreyra Mendes (2001). La elaboración de este problema en la escala más amplia se encuentra en Language Networks de Richard Hudson (2006). Como una manifestación particularmente expresiva de lo que en la especificación epistemológica hemos llamado el principio de Nelson Goodman, en este renglón me parece oportuno contraponer los resultados de un refinamiento en la escala de tratamiento como los que se acaban de ver con los que se manifiestan cuando la escala es más abarcativa. Dando un paso más en el análisis de la distribución de palabras, Tamás Vicsek proyectó la idea al estudio de comunidades, verbales inclusive. Encontró así que la estructura compleja de comunidades parcialmente superpuesta es la misma en diversas clases de redes (de autores, de grupos, de proteínas) y tiene una distribución específica (figura 24; Palla, Derényi, Farkas y Vicsek 2005). Consecuencia n° 9: En suma, los especialistas en redes sociales, circuitos de intercambio, estadística sociocultural o epidemiología de las representaciones harán bien en pensar de nuevo sus modelos tomando en cuenta lo que ahora se sabe y los avances que ha habido en un número crecido de disciplinas. No tenemos aquí una numerología impracticable ni un trasplante conceptual forzado de una ciencia dura a una blanda: más bien sería al contrario, Pareto, Zipf y redes sociales mediante. Lo que sí tenemos es un conjunto de indicadores que podrían utilizarse como heurísticas orientadoras. 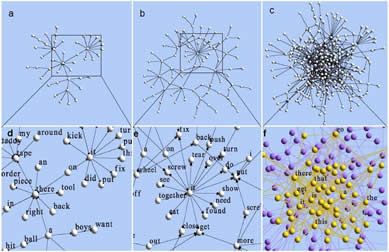Figura 23 – Transición de árboles a red LE En consecuencia, cualquier juicio sobre colectivos sociales, prácticas de comunicación y procesos de cambio debe determinar primero caso por caso la naturaleza de la distribución en la estructura de una red y luego conocer en profundidad las propiedades características de cada una de ellas. Pues en tanto signo a interpretar, cada tipo de distribución es además sintomático de ciertas clases de procesos, de correlaciones y de causas que recién se están comenzando a comprender mejor. Algunas distribuciones son próximas a otras, que quizá sugieran hipótesis alternativas; otras jamás podrían ocurrir en ciertos escenarios. Ningún antropólogo debería dar cuenta de una distribución encontrada en sus datos sin ponerla en el contexto y en el marco significativo de las distribuciones posibles; lo cual contribuiría, de paso, a que se pueda calibrar mejor en qué medida el estudioso domina el campo de posibilidades del fenómeno del cual está tratando. Predigo, en este sentido, que si la teorías de redes LE y las teorías relacionadas continúan su proceso de expansión, se hará necesario que alguien escriba alguna vez un buen manual de distribuciones características en la vida sociocultural15, bien razonado, convenientemente pedagógico, análogo al manual matemático de distribuciones de Evans, Hastings y Peacock (1993) o al precioso compendio de Kalimuthu Krishnamoorty (2006). Ya hay antecedentes de esta iniciativa en al menos una ciencia semiblanda: en economía y ciencias actuariales existen al menos dos volúmenes en esa tesitura, el de Christian Kleiber y Samuel Kotz (2003) y el de Svetlozar Rachev (2003). 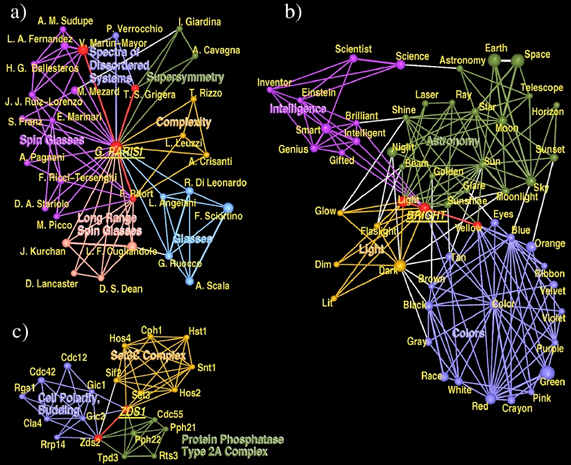Figura 24 – Comunidades Libros así ayudarían a establecer qué clase de distribución (y por qué) es susceptible de esperarse en qué escenarios, y qué clases de universalidad pueden estar detrás de cada perfil estadístico; ayudarían también a pensar las estructuras de manera creativa, a exorcizar algunos fantasmas demasiado buenos para ser verdad (numerologías inspiradas en la constante de Feigenbaum, duplicaciones de período de las ondas cerebrales en las crisis epilépticas, distribuciones mal calculadas en criticalidad auto-organizada, el efímero concepto del filo del caos, fractals everywhere) y a poner un límite, como reclamaba René Thom, a la arbitrariedad de la descripción. 13 – Clases de universalidad y claves para una transdisciplinaPido al lector un ejercicio de paciencia ahora, porque tendremos que incursionar en una física al principio distante; pero en página siguiente y no más lejos veremos cómo, casi teatralmente, la teoría de redes sociales consuma una poderosa integración no reduccionista. En efecto, uno de los aspectos más interesantes de la teoría de redes LE es su vínculo con un conjunto de teorías físicas algo anteriores que luego proporcionarían fundamentos e intuiciones para el conjunto de las ciencias complejas. Esas teorías se refieren a las transiciones de fase de segundo orden, que son las que suceden de modo continuo. En 1965, el físico Leo Kadanoff había determinado que en la vecindad de los puntos críticos, donde ocurren transiciones del desorden al orden o viceversa, diversos sistemas físicos se comportan todos conforme a leyes de potencia. Ese es el principio de universalidad, que rige con independencia de la naturaleza del sistema; la palabra para designar este principio surgió en conversaciones sobre teoría de campo que Kadanoff sostuvo al borde de la borrachera en un bar de Moscú con Sasha Polyakov y Sasha Migdal. La idea de mayor fuerza en esta teoría es que en las cercanías de los puntos críticos sólo existen unas pocas soluciones diferentes a cada problema; muchos problemas en apariencia distintos admiten una misma solución, lo que equivale a decir que pertenecen a la misma clase de universalidad: cambiar el objeto empírico del modelo no cambia los aspectos esenciales de las respuestas. Ahora bien, lo que nos impacta más fuertemente de todo esto es que en los fenómenos críticos las clases se definen a nivel macroscópico, describiendo el tipo de información que el sistema debe transferir sobre distancias largas (en relación con el tamaño de las unidades); en lugar de tratar el sistema en términos de sus unidades mínimas, reductivamente, lo que se hace es determinar una escala más molecular o (parafraseando a Geertz) una descripción más gruesa. Tanto la teoría como los experimentos han demostrado que este scaling es una de las claves de la universalidad y de los fenómenos colectivos tanto en ciencias duras como en ciencias blandas (Kadanoff 1999: 159-160). En dinámica no lineal se dice que los sistemas cuyas transiciones de fase posean el mismo conjunto de exponentes críticos pertenecen a una misma clase de universalidad. En teoría de redes complejas es posible vincular entonces cosas tan diversas como las relaciones personales, la Internet, los ferromagnetos, las citas bibliográficas, la propagación de enfermedades y la percolación (Watts 2004: 65; Miceli 2007). En los estudios de auto-organización se reconocen pertenecientes a la misma clase fenómenos emergentes tales como la formación de patrones ondulados en dunas de arena, las manchas en pelajes o conchas de moluscos, la sincronización de cardúmenes y bandadas, las soluciones autocatalíticas o los nidos de termitas (Camazine y otros 2002). Que objetos de ámbitos tan diversos (al nivel de abstracción y a la escala adecuada) pertenezcan todos a unas pocas clases de universalidad es lo que hace la transdisciplina posible. Sentando las bases de esta posibilidad, el físico Kenneth Wilson de la Universidad de Cornell propuso en 1971 una poderosa teoría unificadora de las transiciones de fase, conocida como teoría del grupo de renormalización, cuyo punto de partida es, una vez más, la invariancia de escala y la universalidad. Esta teoría afirma que las propiedades termodinámicas de un sistema en las cercanías de una transición de fase dependen de un número muy pequeño de factores (tales como dimensionalidad y simetría) y es insensible a las características microscópicas del sistema; a la escala adecuada, es suficiente entonces considerar unos pocos grados de libertad. Esto merece ser dicho en otros términos, vinculándolo con lo que habíamos visto antes. Un escenario común a las ciencias sociales y a las ciencias duras es que ambas lidian con objetos que poseen muchos grados de libertad, que interactúan entre sí de maneras complicadas y en forma no lineal, de acuerdo con leyes o principios que se comprenden pobremente o no se conocen en absoluto. Pero es de algún modo posible hacer progresos en la comprensión de esos sistemas aislando unas pocas variables relevantes que caracterizan la conducta de esos sistemas a una escala particular de tiempo o espacio y postular relaciones de escala muy simples entre ellas. Esto puede servir para unificar conjuntos de datos numéricos y experimentales tomados bajo condiciones muy diferentes, y eso es precisamente la universalidad. Cuando hay una sola variable independiente, las relaciones toman a menudo la forma de una ley de potencia, con exponentes que no parecen ser números racionales simples pero que son, una vez más, universales (Cardy 1996: xiii). Wilson recibió un Premio Nobel por ese logro, e inspiró a Mitchell Feigenbaum en su búsqueda de la constante universal, la cual también describe regularidades independientes de objeto allí donde no se sospechaba que existiera ningún orden. Todo lo que tenía que ver con bifurcaciones y auto-organización quedó incorporado de este modo (en detrimento de la teoría de catástrofes, yo diría) bajo un marco amplio, conexo y elegante, aunque sólo algunos años más tarde estas ideas convergieron con la teoría de redes, la complejidad, los fractales y el caos (Kadanoff 1983: 47; Fáth y Sarvary 2005). Barabási lo expresa de este modo:
Aquí cabe citar largamente un razonamiento aclaratorio y sin desperdicio ofrecido por el padre de la geometría fractal:
La naturaleza de la universalidad en las ciencias complejas ha sido caracterizada por Robert Rosen con inusual agudeza. La ciencia del caos –dice– nos proporciona comprensión sobre la naturaleza en general, independientemente del fenómeno o proceso que estemos observando. Nos permite, por ejemplo, estudiar la turbulencia como una cosa en sí misma, independiente de los fluidos turbulentos específicos. Un observador ortodoxo estudiaría, pongamos por caso, sólo el agua turbulenta, el aire o el aceite turbulento, y en tales casos turbulento sería sólo un adjetivo; un caólogo, en cambio, diría más bien que turbulencia es el nombre de la cosa, y que el fluido particular es el adjetivo modificador circunstancial (Rosen 2000b: 149, 193). Esto es lo que los transgresores Jack Cohen e Ian Stewart (1994: 442) conciben como “complicidad” (= complejidad + simplicidad) entre inteligencia y exteligencia: la ocurrencia del mismo rasgo emergente en sistemas de distinta materialidad. Algo muy parecido a esto es también lo que Gregory Bateson llamaba la pauta que conecta. Consecuencia n° 10: Por razones de espacio debo dejar a un lado una de las propiedades de las redes LE de consecuencias más amplias y ricas, nada menos que su fractalidad, con lo que se nos escapa también gran parte de la dinámica no lineal en general y del caos determinista en particular. Ya habrá ocasión, en futuros estudios, de explorar regiones de las ciencias de la complejidad y el caos que aquí apenas se han alcanzado a insinuar (cf. Reynoso 2006). No obstante, es necesario remarcar que, al contrario de lo que se ha afirmado tantas veces, la dimensión fractal (o el carácter relativo de la medición de formas complejas) no involucra incertidumbre, ni indeterminación, ni azar, ni subjetividad, ni un efecto Hawthorne introducido por el observador. Aunque una dimensión fraccional suene como un concepto extraño y las curvas fractales hayan sido durante tanto tiempo llamadas “monstruosas”, la medida de los objetos fractales es una función estrictamente relativa a la unidad de medida (Edgar 2008: 165-223). Consecuencia n° 11: Éste concierne nada menos que a una nueva definición de universalidad y a un concepto razonablemente más articulado de transdisciplina de lo que hasta ahora ha sido la pauta en ciencias sociales. La transdisciplina es posible porque las estructuras de los problemas son pocas y son las mismas en todas partes, y no porque los especialistas se sienten a negociar y digan lo que saben sobre objetos que los demás no entienden. Matemáticos abstractos y sociólogos de lo concreto pueden hablar un mismo idioma por poco que ambos planteen sus problemas, por ejemplo, en términos de redes o de complejidad. Esto no es una expresión de deseos; la prueba tangible de la fecundidad de esta aproximación es hoy en día abrumadora. Consecuencia n° 12: Finalmente hay que hacer alguna referencia a los problemas simétricos de la reducción y la emergencia. La perspectiva transdisciplinaria que aquí se formula no tiene nada que ver con una ciencia líder o con una “teoría de todo” a cuyas unidades mínimas las ciencias de objeto más englobante o nivel de inclusión mayor deban rendir tributo. Los átomos, los componentes y las partículas elementales (sean de la física, la significación o el parentesco) son propios de los modelos mecánicos, no de los complejos. Lo que yo encuentro cuestionable es que se utilice una clase de modelos para cuestionar otra. Sobre todo en el lado humanístico de la divisoria se ha exagerado grandemente el carácter perverso de la reducción; se ha ofrecido con demasiada prodigalidad la idea de emergencia como un antídoto anti-reductor, una especie de epistemología no lineal apta para toda ocasión, una solución de apurada cuando surgen escenarios que la teoría no ha sido capaz de predecir. Pero incluso en las ciencias formales se están dejando atrás las actitudes conspirativas, místicas o triunfalistas y se está abordando de manera teoremática la problemática intensamente filosófica de la emergencia (Crutchfield 1994; Christen y Franklin 2002; Kubík 2003; Shalizi y Moore 2003; Boschetti y otros 2004; Hatcher y Tofts 2004). El tema se está poniendo complicado y todavía la cuestión no se ha asentado en un estado estable ni se ha escrito un manual recomendable sobre ella que no vaya a quedar caduco en breve. La tensa relación entre reducción y emergencia es demasiado complicada para tratarla en este punto, pero yo diría que su dialéctica depende de las formas de representación y no es tan sintomática de lo complejo como lo son, por ejemplo, la no linealidad y la sensitividad a las condiciones iniciales. Esta lección, que es más bien una expresión de deseos que un corolario, concierne a la necesidad de reprimir la tendencia a pontificar sobre cuestiones técnicas y epistemológicas de indecible complejidad, como lo son hoy en día las que tienen que ver con la aleatoriedad, la reducción y la emergencia. 14 – Criticalidad auto-organizada y PercolaciónTras el nombre engorroso de criticalidad auto-organizada se esconde una idea de seductora simplicidad que ha dado lugar a una explosión de investigaciones en un número crecido de disciplinas. El fundador de la especialidad, el dinamarqués Per Bak [1948-2002], fue un personaje carismático que apostó a una intuición genial, a una denominación con las palabras justas y a un golpe de efecto; pero el éxito de la idea no se debió sólo a eso. En la física clásica, un punto crítico es un punto en el cual un sistema cambia radicalmente su conducta o su estructura, por ejemplo, al pasar de sólido a líquido. En esos fenómenos críticos normales, existe un parámetro de control que el experimentador puede variar para obtener ese cambio. En el caso del sólido que se derrite, el parámetro de control es la temperatura. En los fenómenos críticos auto-organizados, en cambio, los sistemas alcanzan un punto crítico de acuerdo con su propia dinámica interna, independientemente del valor de cualquier variable de control. La idea crucial de Bak consistió en pensar que el arquetipo de un sistema crítico auto-organizado bien podría ser una simple pila de arena. Arrojando un hilo de arena lentamente sobre una superficie se forma una pila. A medida que la pila crece, ocurren avalanchas que transportan arena desde la cúspide hasta la base. Al menos en los modelos teóricos, la pendiente de la pila es independiente de la velocidad en que se arroja la arena. Esta es la pendiente auto-organizada, que se llama así incluso en casos en los cuales la pila no tiene forma de cono o adopta una configuración irregular. En los sistemas de este tipo, un evento menor (un grano de arena adicional) puede desatar una reacción en cadena: el mejor ejemplo de una función no lineal. Estas ideas fueron propuestas por Per Bak a principios de la década de 1990 y encontraron acogida permanente en las ciencias del caos, aunque el propio Bak fue más bien partidario de las ciencias de la complejidad (Bak 1994; 1996; Bak y Chen 1991; Jensen 1998). Tienen la virtud invalorable de arrojar luz sobre el escurridizo concepto de auto-organización: la conducta de la pila de arena depende de la interacción entre los elementos y no de un control exterior. Dado que el estado de la pila determina cuánta más arena hace falta para alterarla, un grano de arena puede tener una influencia desmesurada o no tener ninguna; la magnitud de la influencia está determinada por el estado actual, pero el estado siguiente está determinado por el grano de arena. Las avalanchas involucran a los elementos interactuantes en la pila, según las relaciones de comunicación y vecindad que mantengan entre sí. Aquí ya podemos entrever una primera analogía con el concepto de red. El tamaño y frecuencia de avalanchas (como los de los terremotos y los motines) parece obedecer a una distribución de ley de potencia, semejante a la ley de Zipf y a la ley de Pareto: los eventos pequeños son los más frecuentes, y los grandes los menos. Cuando se grafican las distribuciones de ley de potencia no resultan en el familiar histograma gaussiano campaniforme, sino en una distribución lineal que desciende brusca y monótonamente desde los valores más altos a los más bajos. La ley de potencia es una característica fractal (presente por ejemplo en el número de ríos que confluyen en una cuenca en relación con sus respectivas longitudes) que se encuentra en muchos ámbitos diferentes como la economía, la biología, la física y al parecer la cultura, sin que exista aún una teoría universalmente aceptada que explique su ocurrencia. Más allá de la atmósfera ideal de los laboratorios, los investigadores de SOC se concentraron en sistemas naturales y sociales de los que se sabía que exhibían comportamientos invariantes de escala. Aunque muchos de esos estudios fueron resistidos por los especialistas convencionales, a la larga la SOC se impuso como un fuerte candidato para la explicación de un gran número de fenómenos, incluyendo terremotos (ley de Gutenberg-Richter), secuelas sísmicas (ley de Omori), manchas solares, fluctuaciones en mercados financieros y otros fenómenos de la naciente econofísica, ondas de pánico y formación de paisajes (Tamás Vicsek), incendios forestales, epidemias, evolución biológica (sobre todo en relación con las teorías del equilibrio puntuado de Niles Eldredge y Stephen Jay Gould) y por supuesto guerras. Cuando surgió con fuerza el análisis de redes libres de escala, se propuso también un número de modelos de SOC para generar tales redes como fenómeno emergente (Paczuski 2005). Hay una pequeña pero entusiasta comunidad de analistas de redes sociales que ha acogido con simpatía estas ideas de Per Bak, las cuales han encontrado cierta resistencia debido a aspectos dudosos de su elaboración matemática original. Entre los estudios que vinculan SOC con redes sociales destacan los de Gérard Weisbuch, Sorin Solomon y Dietrich Stauffer (2003) y los de Steyer y Zimmermann (2000). La literatura sobre SOC en antropología y demás ciencias sociales es ya de volumen considerable, pero dado que en su mayor parte no se refiere a modelos de red no la iremos a tratar aquí (cf. Reynoso 2006: 290-303). Por su parte, la teoría de la percolación tiene harto mejor imagen y fundamentación formal que la criticalidad y un atractivo que no le va en zaga. Surgió hace unos cincuenta años para estudiar algo tan aparentemente ligado a un fenómeno como lo es el paso de un líquido a través de un medio poroso desordenado, o sea con canales bloqueados al azar. Dos ingleses, un matemático y un ingeniero, estaban estudiando bajo qué circunstancias se obstruye el filtro para la entrada de aire en las máscaras de gas (Broadbent y Hammersley 1957). Con esas máscaras se puede respirar bien mientras las impurezas (polvo, esporas, insectos) no se acumulen tanto que obstruyan los conductos del filtro. Los investigadores encontraron que la respuesta no es proporcional, ni gradual; en un momento se puede respirar más o menos bien, en otro momento se obstruye la entrada de aire por completo. Por encima de un 40% de conductos obturados (o de una cifra en ese orden de magnitud), la corriente de aire se corta en seco. Hay un antecedente a esas investigaciones que traen la problemática a un terreno más familiar y que tiene que ver con los estudios de Paul Flory [1910-1985] y Walter Hugo Stockmayer [1914-2004] sobre gelación durante la Segunda Guerra Mundial. Este proceso describe cómo se forman macromoléculas entre pequeñás moléculas ramificadas a medida que se forman vínculos químicos entre éstas. Cuando este proceso de polimerización cubre todo el sistema se habla de gelación. Todos los que han calentado un huevo para hacer un huevo cocido han experimentado algo parecido. El estado de la albúmina puede ser o bien líquido o bien como el de un gel (de allí lo de gelación); no hay estados intermedios. Cocer un huevo puede pensarse como un proceso de percolación sobre un enrejado de Bethe o un árbol de Cayley (Stauffer y Aharony 1994: 4). Hay otro antecedente mucho más temprano que demuestra, por si hiciera falta, el carácter contraintuitivo que tienen estos procesos de transición de fase. El geógrafo griego Estrabón cuenta que en su época la península ibérica estaba tan poblada de árboles que una ardilla podía pasar del cabo de Gata a Finisterre sin tocar el suelo, saltando de un árbol a otro. Durante siglos, los ecologistas pensaron que España al menos era un denso bosque; algunos hasta creyeron que Estrabón exageraba, o que los salvajes túrdulos, carpetanos, bástulos u otros pueblos igualmente desaprensivos (de ningún modo los apolíneos celtas) con el tiempo dieron cuenta de los árboles. Pero el error de toda esta hermenéutica consiste en creer que para que la ardilla pueda ir de un extremo al otro todo el país tendría que estar cubierto de vegetación. La teoría moderna de la percolación demuestra, por el contrario, que con algo más de la mitad del terreno forestada ya se podría hacer ese recorrido (Segarra 2001: 236). Figura 25 – Percolación de ligamento (basado en Grimmett 1999: 4, 5) A diferencia de la teoría que examinamos antes, en la actualidad la forma normal de expresión de las teorías de la percolación (se refieran a líquidos, fuegos, enfermedades, rumores, modas, consignas o lo que fuese) es la teoría de grafos, redes inclusive (Bollobás y Riordan 2006). Hay leves diferencias terminológicas por cierto. Los vértices y los arcos se llamen sitios [sites] y enlaces [bonds]; cuando se obtiene un grafo seleccionando nodos se habla de percolación de sitio; cuando se seleccionan los arcos, percolación de enlace. Hay una tercera clase, percolación continua, que se está comenzando a comprender mejor. Hay especialistas en percolación de uno u otro tipo, pues su relación es complicada; algunos de aquéllos a veces abrazan su modalidad de percolación favorita de maneras casi apasionadas. Si bien puede que rechine el cerebro cuando se lo piensa, es evidente que todo modelo de enlace se puede reformular como un modelo de sitio sobre una grilla o enrejado [lattice] diferente; pero lo inverso no es verdad: los modelos de sitio son entonces más generales. La figura 25 muestra dos procesos de percolación de enlace para p = 0.49 y p = 0.51; en el segundo caso a la derecha hay percolación horizontal; en el primero no. Como es propio de la percolación de enlace, los bloqueos están asociados con discontinuidad de las líneas. Con el correr de los años la teoría de la percolación ha constituido una especialidad en sí misma con objetos dispersos en múltiples disciplinas, con la física en primer lugar. Sus problemas inherentes, que parecieran de formulación sencilla, no admiten en general soluciones analíticas simples. Como dice Geoffrey Grimmett (1999: viii), la disciplina, cuyo crecimiento se mide a escala de horas, tiene fama de ser tan dura como importante. En definitiva, lo importante es que las teorías de la percolación y de la criticalidad auto-organizada, cualquiera haya sido su fortuna en la antropología en general y en el ARS en particular, están claramente interrelacionadas. Las principales nociones son las mismas en ambos campos: fractalidad, umbral crítico, transiciones de fase, invariancia de escala, exponente crítico y auto-similitud para empezar. Algún día el analista de redes se encontrará con alguna de esas teorías en el camino, y es mejor que vaya tomando nota de lo que le espera. Consecuencia nº 13: En diversos regímenes teóricos las epidemias, igual que las redes, han ofrecido aquí y allá metáforas para imaginar procesos comunicativos en particular y sociales en general. La antropología lidia desde hace un tiempo con la paradoja de que su mejor modelo epidemiológico, o al menos el más conocido, el de Dan Sperber (1994; 1996; 2000; Sperber y Wilson 1986) desenvuelve un modelo de replicación evolutiva que no es el habitual en las ciencias de la complejidad, donde prevalecen los algoritmos evolutivos, la memética o la teoría evolucionaria a secas; promueve también un modelo epidemiológico que no guarda relación con las teorías de la percolación o con el análisis de redes sociales y un modelo cognitivo que no incorpora prácticamente nada de la ciencia cognitiva o la neurociencia cognitiva social contemporánea. Una y otra vez, entonces, en la disciplina se pierden oportunidades, se promueve el modo privado de producción teórica y se reinventa la rueda en cada ocasión que se desenvuelve teoría. Estamos en presencia de otro anti-patrón característico: tampoco la comunidad de ARS ha formalizado por completo su relación con dos campos importantes de las teorías complejas, como lo son las teorías de la criticalidad auto-organizada y la percolación. En agudo contraste con este diagnóstico, al lector le habrá resultado evidente que existe una analogía no trivial entre los asuntos tratados en este capítulo y los desarrollados en el resto del ensayo; la aparición de un conglomerado infinito pasando el umbral de percolación, por ejemplo, es lo mismo que la aparición de un componente gigante en un grafo aleatorio ER. La robustez ante fallas al azar de una red equivale a la comunicabilidad dentro de un componente gigante y al proceso de percolación de sitio. La geometría de todos estos procesos es fractal. A esta altura del ensayo está claro que un tema por completo ligado a un asunto peculiar puede esclarecerse a partir de los problemas de la misma clase que se encuentran en otros dominios. Resultaría forzado investigar con formalismos de redes asuntos que requieren una aproximación de orden narrativo o estético; pero en los asuntos que claman por una visión como la que las redes y la complejidad ofrecen, son las visiones tradicionales de la antropología, lógicas concretas ligadas al objeto, las que tienen que probar su relevancia y dejar un espacio a las nuevas exploraciones. 15 – Parentesco: Nuevas técnicas reticularesSi se quisiera hacer cabal justicia al objeto, científicamente hablando, no estaría de más asomarse al estado del conocimiento en el desarrollo de instrumentos de alcance abstracto o de propósito general. A título de experimento crítico invito ahora a examinar el caso de lo que ha sido durante un siglo el objeto más peculiar de la antropología; una vez pesada la evidencia, también propongo comenzar a pensar lo que podría lograr esta disciplina si llevara a la práctica con mayor consistencia y reflexividad esa clase de examen. Es bien sabido que el estudio del parentesco en antropología ha dejado de ser lo que era. Hace tiempo que no es el enclave privilegiado de los debates teóricos de la disciplina. Sometido a fuego crítico a mediados de la década de 1960 desde dos o tres puntos de ataque, su derrumbe fuera de toda proporción, junto con la paulatina pérdida de las habilidades comparativas, ha convertido a la antropología en una disciplina con un perfil muy distinto del que tenía (digamos) hace unos cuarenta años. No viene al caso referir las razones de la impugnación del parentesco, ni los dictámenes pesarosos sobre el estado del problema, ni los contrastes que median entre la perspectiva norteamericana y la europea (la cual todavía resiste o languidece), ni las formalizaciones que han venido al rescate pero que no se atienen al paradigma reticular. La bibliografía es masiva y sólo puedo hacer constar aquí las referencias más imperiosas, algunas con títulos de apocalipsis tan expresivos que da cierta lástima no poder seguir sus alegatos (White y Jorion 1992; Peletz 1995; Collard 2000; Fogelson 2001; Lamphere 2001; Kuper 2003; Sousa 2003; Carsten 2004). Lo que se impone es indagar la notación genealógica y sobre todo la analítica que le está asociada. ¿Qué pasa con ellas? En una época nadie sabía modelar el parentesco con tanta solvencia como un antropólogo; hoy esa virtud pasa por otras coordenadas disciplinares y por otras nomenclaturas: no se habla ya de parentesco sino de familia, y género significa algo distinto a lo que acostumbraba significar. Hasta la revista Man ha cambiado de nombre, recuperando su no menos anacrónico título de Journal of the Royal Anthropological Institute. Lo lamentable es que las habilidades se perdieron en un mal momento, justo cuando en casi todas las sociedades se manifestan “nuevas formas familiares” y nuevas tecnologías de la procreación. Otra oportunidad desperdiciada, otro antipatrón, si cabe. Aún cuando los antropólogos recuperen las capacidades perdidas no podrían volver a su sitial, pues hoy se sabe, a la luz de lo que nos enseñado las redes y los grafos, que las técnicas genealógicas tradicionales carecían de rigor, de capacidad descriptiva, de agudeza diagnóstica, aún en términos de pura antropología y de puros significados. Con toda su pretensión de estado de arte eran un lastre victoriano, técnica e ideológicamente. Es curioso, pero ni la crítica simbólica de David Schneider (1984) ni la más epistemológica de Rodney Needham (1971) habían puesto en cuestión la herramienta analítica o la terminología de orden técnico. Las impugnaciones eran de otro orden y concernían más a la categoría misma de parentesco como fenómeno cultural o como objeto de estudio que a los instrumentos con que se organizaban los datos. Liberados del peso de la prueba gracias al criterio de autoridad, los epígonos de Schneider y Needham fueron por supuesto más lejos, y con los años quedó flotando la impresión de que seguir estudiando el parentesco podría llegar a ser decididamente superfluo, reaccionario o imbécil. En los noventa se volvió costumbre afirmar que no existía el parentesco, o los universales de la procreación, o los linajes, o la cultura, o nada. 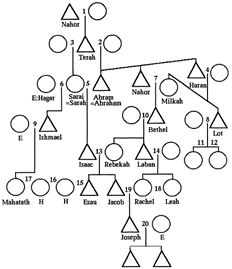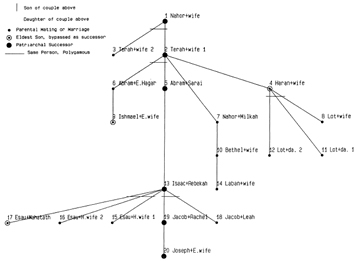Figura 26 – Genealogía de Canaán - Diagrama genealógico y grafo parental (s/ White y Jorion 1992: 455-456) Pero incluso los antropólogos que pensaban que la crítica era excesiva, o que obedecía a propósitos oscuros, creían que la centenaria notación y la rica nomenclatura técnica de la antropología clásica funcionaban más o menos bien. Nunca fue así, por desdicha. Todavía se la enseñaba acríticamente no hace tanto tiempo; hoy todo el mundo se da cuenta (o debería hacerlo) que no hay una analítica fuerte que sirva de respaldo a la diagramación y que como técnica de representación gráfica la diagramación genealógica apesta. Los diagramas genealógicos son por otro lado un camino sin salida, pues están demasiado adheridos a una interpretación sustantiva en términos de alianza, filiación y consanguinidad. En ambientes de redes hay un par de modelos gráficos posibles (el que se usa por defecto son los gráficos-ORE) y a nadie se le ocurriría mirar el sistema como un gráfico de resortes, o calcular otras nociones que la que aprendió a pensar cuando de parentesco se trata. Escribía hace unos años el mayor especialista en redes de parentesco, Douglas R. White:
Aunque los diagramas estándar parezcan un dispositivo neutro para representar individuos, sus matrimonios y su descendencia, ellos están afectados por un individualismo metodológico inherente, el cual se encuentra en concordancia con las teorías sociales, políticas y económicas del mundo anglosajón. Los antropólogos las siguen usando, prosiguen White y Jorion (loc. cit.), aún cuando esos diagramas resultan confusos cuando se quieren mostrar elementos de la estructura social de las comunidades o las familias que están vinculadas por matrimonios cruzados o por ancestros comunes, y aún cuando casi no sirvan para hacer los cálculos, las búsquedas o o las transformaciones que en otras formas de representación en red son rutina. La crítica de Bouquet (1993) también subraya la especificidad cultural del método genealógico, argumentando que estaba imbuido de nociones inglesas de pedrigree (explícitas en los trabajos de Rivers), muy poco parecidas, por ejemplo, a las categorías portuguesas de relación parental. 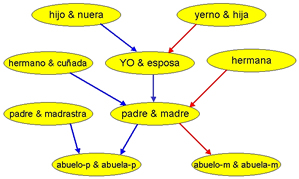Figura 27 – P-Graph La solución propuesta por White consiste en la implementación de P-Graphs, un nombre no vacante que puede llevar a confusión y que se usa con otros sentidos en marketing o en lingüística. En realidad no interesa cuál sea la técnica en particular; lo importante es que engrane con el análisis de redes, con teoría de grafos y con álgebra lineal y que posea por ende el mismo carácter de sistema analítico abierto que los instrumentos que hemos entrevisto. Una vez que uno tiene una red posee por añadidura todo lo demás: los cálculos de propiedades, las matrices con sus álgebras, las herramientas de comparación, la minería de datos, las técnicas de descubrimiento de patrones, las prestaciones de animación y estudio diacrónico, la posibilidad de vincular la genealogía a otros datos reticulares, todas las visualizaciones imaginables. Y si este es el temor del estudioso cualitativo pegado a su objeto, ni hablar de lo que sucede a nivel de las prestaciones específicas de parentesco: la posibilidad de encontrar casamientos entre hermanastros o hermanastras, la de representar casamientos sucesivos, la de comparar regímenes y frecuencias de patrones de re-encadenamiento de distintas genealogías Cuando se lo comienza a usar el P-Graph puede resultar contraintuitivo porque los nodos son parejas o personas solteras; como es un grafo acíclico no hay arcos que unan a los padres, y los únicos arcos que hay van de los hijos a los padres (figura 27). Una variante bipartita de P-Graph posee vértices rectangulares para denotar parejas, y, como en los viejos tiempos, círculos para representar mujeres solteras y triángulos para varones solteros. A menos que se den instrucciones en contrario el grafo corre de abajo hacia arriba, al revés de lo que los antropólogos (contrariando a genealogistas y a matemáticos) piensan que debería ser el caso. En genealogía se piensa en árboles que crecen de abajo hacia arriba, mientras que en antropología el proceso temporal se concibe como un proceso de descendencia. Sea como fuere, en los P-Graphs la textura es tan espartana que al principio da la impresión de que hay menos datos que en los viejos diagramas, pero no es así; en realidad hay muchos más. Pero las ventajas de estas metodologías son múltiples y ratifican el hecho de que una técnica robusta no aniquila la especificidad del objeto ni lo torna enrarecido, sino que descubre en él infinidad de nuevas perspectivas. Por empezar, un formalismo como el P-Graph no presupone clausura generacional en el tiempo, ni la unidad del grupo parental; por el contrario, facilita el análisis longitudinal del cambio de las relaciones de parentesco y permite visualizar las redes desde tantos ángulos y en función de tantos filtros, criterios y acentuaciones como se quiera. Al costo de una noche de aprendizaje, se podrán representar con él reglas de matrimonios simples y complejas, evitación del incesto, ciclos matrimoniales, segundos, terceros o enésimos casamientos, poligamia y poliginia, grupos endogámicos y exogámicos, diferencias en tiempos generacionales entre hombres y mujeres y sus efectos en la estructura, las consecuencias del casamiento poligámico, la integración de parientes clasificatorios, las transformaciones de status por crianza o lactancia, el cambio histórico en la constitución de la familia, la adopción por parte de parejas hetero u homosexuales, etcétera. Una técnica alternativa a los P-Graphs es la de los modelos de bloque (White, Boorman y Breiger 1976). La idea del modelado en bloque fue creada por François Lorrain y Harrison White (1971) a partir de la tradición de análisis algebraico de parentesco iniciada por André Weil en su legendario apéndice para Las estructuras elementales de parentesco de Claude Lévi-Strauss (Weil 1985; Courrège 1965). Puede decirse que estos modelos utilizan grafos casi en el sentido familiar de la palabra, pero sólo en la construcción de una nueva entidad que una vez construida deviene objeto de análisis. Eso permite no ya derivar índices como sucede en los grafos normales, sino usar algoritmos para identificar inductivamente roles a partir de los grafos. Estos roles se pueden a su vez articular en complejas estructuras de rol mediante técnicas algebraicas, las más de las cuales giran en torno del concepto de equivalencia estructural. El objetivo del modelado en bloque es reducir una red grande, potencialmente incoherente, a una estructura menor de interpretación más sencilla. El procedimiento se basa en la idea de que las unidades de una red se pueden agrupar en la medida en que sean equivalentes, conforme a una definición significativa de equivalencia. Una tercera técnica de recambio para diagramación de parentesco ha sido propuesta hace tiempo por Brian Foster y Stephen Seidman (1981), coordinando el modelo más rico y complejo de genealogía antropológica (que por un amplio margen es el de Meyer Fortes) con los formalismos de grafos y el análisis de redes concomitante. Otro modelo poderosísimo es el KAES (Kinship Algebraic Expert System) desarrollado por Dwight Read, capaz de construir un modelo algebraico de la lógica subyacente a un sistema de parentesco (Read y Behrens 1990; Read 2001); pensado como un modelo de Inteligencia Artificial y cálculo de predicados a la antigua usanza, su relación o su posible compatibilización con el análisis de redes es todavía oscura. No digo que la disponibilidad de estas herramientas o de otras parecidas habría podido detener el proceso de deterioro de la antropología científica; hubo otros factores mucho menos ligados a los temas de interés o a los predicamentos internos de una disciplina que estaban globalmente en juego. Lo que sí digo es que si se quieren investigar problemáticas complejas de la familia, del parentesco, de los grupos, las sociedades o lo que fuere, se tiene ahora por lo menos algo un poco más sólido por donde empezar. En el apogeo de la declamación y el radicalismo antiteórico en antropología llegó a parecer que el estudio del parentesco es por necesidad un ejercicio bizantino. Está claro que no lo es; no siempre al menos. A despecho de las críticas de la época, ellas también criaturas de sus tiempos, las genealogías han llegado a ser una herramienta poderosa de reclamo identitario personal, cultural y hasta territorial. En Internet se están gestando los primeros mapas genealógicos de la humanidad y en el mundo descolonizado se está redescubriendo en función de ellas parte de su historia. El método se ha manifestado esencial en estudios de etnohistoria y de antropología rural no necesariamente anecdóticos y hasta en la organización de materiales de museo. El uso de las genealogías relevadas a partir de la expedición de la Universidad de Cambridge de 1998 por parte de los nativos ha modificado los patrones de tenencia de la tierra entre las comunidades aborígenes australianas y en el Estrecho de Torres, que no por nada es el lugar donde el método genealógico se originó (Segalen y Michelat 1991; Bouquet 2001). El impacto de las nuevas tecnologías genealógicas y los nuevos usos de las genealogías desarrolladas en el pasado por los antropólogos son dos de los usos que, a despecho de todas las críticas, podrían situar el método más en el futuro que en el pasado de la disciplina. Consecuencia n° 14: Las herramientas no califican como teorías, aunque puedan estar al servicio de ellas. No importa cuan seductor y fructífero parezca un instrumento, una técnica está muy bien en el lugar que le cabe pero no satisface un rol teórico, como aprendimos por la vía cruel en nuestra disciplina cuando se intentó la aventura del análisis componencial. Aunque ahora se sabe, por ejemplo, que los diagramas de parentesco usados durante un siglo en antropología constituyen una técnica limitada y que hay otros formalismos reticulares de recambio mucho más adecuados al objetivo, esas herramientas todavía están esperando que alguien haga con ellas siquiera una pequeña parte de lo que nuestros antepasados antropólogos hicieron con lápiz, papel, una red de intercambio inexistente y una notación impropia (Foster y Seidman 1981; Collard 2000). Las herramientas están ahí y no son poca cosa, a la luz de lo que la posibilidad de su uso nos ha enseñado. Pero cualquiera sea ahora la capacidad técnica y el aprendizaje epistemológico a los que ella nos ha abierto, el verdadero trabajo teórico está todavía por hacerse. 16 – Alcances y límites de la teoría de redes (y de la complejidad)Mientras
que las ciencias sociales son vistas por Peter Mika (2007: 29) Ya hemos dejado constancia de la significación de la convergencia entre el ARS y las teorías de la complejidad en el tratamiento de las consecuencias epistemológicas emergentes. En cuanto al lado negativo, como bien reza uno de mis artículos favoritos en ingeniería de software, tanto en tecnología como en ciencia “no hay balas de plata” (Brooks 1975). Cuando lo único que se tiene es un martillo, dice otro adagio, todos los problemas se perciben como clavos. La teoría de redes, como cualquier otro principio algorítmico, aunque a veces suene demasiado buena no siempre resulta ser verdad; tampoco garantiza resultados si el diseño investigativo no está a la altura de lo que se requiere, lo cual sucede con inquietante frecuencia. Algunas de las habilidades técnicas requeridas por su analítica son cualquier cosa excepto fáciles y buena parte de las teorías de la complejidad y el caos ha venido a agregarse a lo que hay que aprender. Por conveniente que resulte la metáfora reticular algunas problemáticas resultan mejor tratadas de un gran número de otras maneras posibles. La crítica implacable que realizara Jeremy Boissevain a fines de los setenta incurre en gestos gastados y expresiones de sentido común, pero en sus mejores momentos parece escrita ayer y todavía se mantiene:
Si se observa la relevancia que el análisis de redes ha tomado en el conjunto de las teorías de la complejidad y el caos, se comprobará que incluso las manifestaciones de ARS que en antropología son marginales se han vuelto temas de punta en la escena transdisciplinaria (cf. White 2001; Mitchell 2006; Durrett 2007; Mika 2007). Debido a esta preponderancia y al hecho de que se está viviendo una etapa de deslumbramiento, la reflexión epistemológica devino una especie rara. Casi siempre se trata al ARS como si fuera la única técnica a la vista cuando a veces sería mejor que cumpliera un papel más discreto, como un instrumento entre otros. Recién en los últimos años los estudiosos de redes han comenzado a elaborar reflexivamente el problema de los alcances, los constreñimientos, los usos fetichistas de la tecnología, la diagramación y la publicación de matrices del tamaño de sábanas como fines en sí mismos (Granovetter 1990; Miceli 2008). Dado que el espacio se agota, invito a pensar en estos dilemas y a revisar la bibliografía indicada. 17 – Conclusiones Nadie ha sugerido que la tarea
sea simple, o que Whitten y Wolfe (1973: 740). Ignoro si estamos o no en presencia de un nuevo paradigma radical, como algunos han pretendido, pero es seguro que los desafíos que hasta aquí he planteado requieren al menos una discusión detenida aunque se llegue a ellos por caminos distintos de los que señalé. Habrá que repensar ideas tan solidificadas como las de red, sistema, modelo, problema, pregunta, elicitación, técnica, solución y estadística, y formular de nuevo casi todas las cuestiones aparejadas por la auto-organización, la dimensión fractal, las distribuciones de ley de potencia y la no-linealidad. Una teoría reductora, como la autopoiesis (que por definición sólo debería aplicarse a cosas vivas) no sirve de mucho en este contexto; las analogías epistemológicas se saben ahora más definitorias que las afinidades ontológicas, pues entre tanto hemos caído en la cuenta que aún éstas son siempre conceptualmente construidas. Para emplear una metáfora que los propios complejólogos interpretativos han usado alguna vez, podría decirse que lo que aquí cuenta son los verbos, no los sustantivos, pues son los verbos los operadores conceptuales que permiten activar genuinamente los modelos. A diferencia de los viejos modelos manuales o mentales, los de ahora son por un lado manejables e intercambiables y por el otro autónomos y hasta insumisos. Mientras que antes casi no había herramientas, hoy abundan más allá de lo que se podría llegar a aprender, y como aprendedor compulsivo lo afirmo; se las consigue, gratis, a través de una Web que es ella misma una red concreta, vital, tangible, inmensa y ahora, al fin, inteligible, mucho más de lo que se pensaría que puede llegar a serlo algo tan abismalmente complicado. Los investigadores veteranos deberán aprender de qué se trata o hacerse discretamente a un costado. Ni sueñen que esto pueda resolverse salteándose obtusamente el aprendizaje de todo lo que huela a algoritmos o citando una penosa frase de Edgar Morin en contra de la hiper-especialización. Nadie dice que el álgebra combinatoria, el análisis espectral o la teoría de grafos sean simples, pero los conceptos básicos de análisis de redes se pueden aprender en un mes combinando una docena de los mejores libros con Wikipedia; todos los programas existentes están orientados a usuarios y resultan familiares en un par de semanas de trabajo intenso. De ahí en más se puede ir creciendo de a poco, una idea a la vez. Esos desarrollos no son perfectos y la distribución de la calidad de libros y artículos sobre redes y complejidad exhibe una caída de ley de potencia; pero no es por aquí donde impera la ciencia oscura. La ciencia de las redes del siglo XXI define entonces un concepto de transdisciplinariedad mucho más fructífero y concreto de lo que propusiera Edgar Morin, por ejemplo, quien si bien popularizó el término, nunca imaginó que éste denotara algo más que una reunión de científicos cada uno de los cuales conoce un solo objeto específico y domina un solo lenguaje impenetrable a los extraños. En este espacio no hay lugar tampoco para la vieja jerarquía de las ciencias. La nueva concepción ha sido perfectamente descripta por Duncan Watts:
En el campo interdisciplinario del análisis de redes, los estudiosos de las ciencias sociales han tenido las más de las veces la iniciativa.
Consecuencia nº 15: Ya no es el caso que las ciencias sociales deban resignarse a importar dócilmente conceptos originados en ciencias mejor consolidadas. En el escenario actual lo contrario es harto más probable, aunque son cada vez menos los que piensan en términos de contraste entre prácticas de diversa calidad inherente. En las nuevas disciplinas de redes y complejidad las ciencias sociales tienen hoy una considerable cuota de iniciativa. Tal vez la tuvieron siempre y lo que falló fue una reflexión epistemológica que le hiciera justicia, una mirada que supiera ver más allá de los mitos alentados por algunas escuelas. La gesta del análisis de redes, después de todo, no comenzó ni en las matemáticas abstractas, ni en la práctica de los métodos formales, ni en las ciencias de la computación; comenzó, sin dudas, en la psicología, e incluso en formas de la psicología (psicodrama, teoría de campo) que en algún momento se pensó seudocientíficas, rudimentarias o desprestigiadas (v. gr. Gardner 1988: 574). Lo cierto es que familias enteras de algoritmos en tecnología de punta y métodos formales están esperando inspiración de las ciencias sociales, la cual ha llegado hasta hoy bajo la forma de algoritmos culturales, ingeniería del conocimiento para la Web semántica, heurísticas de sentido común para la inteligencia artificial en estado de arte, computación existencial heideggeriana o fenomenológica, métodos de enjambres de partículas (particle swarms), códigos de la biología copiados de la lingüística, jerarquías de la complejidad (y fundamentos de lenguajes formales) inventados por lingüistas, sistemas de posicionamiento global que emulan el etak nativo de Micronesia, ideas de invariancia de escala pensadas en el estudio de los conflictos humanos, nociones estéticas y estilísticas en arquitectura de software y, por supuesto, teoría de redes sociales, entre otros muchos objetos de intercambio bien conocidos en ciencias duras que las ciencias blandas se obstinan en ignorar. Para finalizar, no quisiera dejar de lado el tema de la importancia política del asunto. Sin ánimo de dramatizar la situación, está claro que el campo de las redes sociales es uno de los muchos en los cuales está en juego (y tiene oportunidad de manifestarse) la relevancia que podría tener la antropología en la comprensión de la dinámica del mundo actual. Saber, por ejemplo, cuál es la distancia geodésica entre George W. Bush y Osama Bin Laden (o la díada que a alguien se le ocurra), o determinar qué es lo que debe hacerse para impedir o impulsar con efectividad la difusión de un virus, un rumor, una campaña, una moda o una política de cooptación, o cómo debe actuarse para proteger un recurso o hacer que colapse un sistema de comunicación, todo esto es cualquier cosa menos trivial. 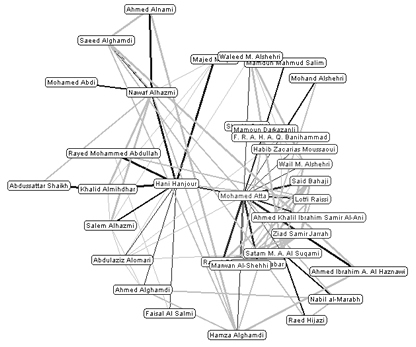Figura 28 – Red de complotados del 11 de setiembre (Network Workbench) Algunos personajes emergentes difíciles de catalogar han hecho fama y fortuna en este campo, brindando servicios de consultoría cuyo valor oscila, a ojos vista, en un rango que va de la razonabilidad a la estafa, con énfasis en esto último. Uno de los más conocidos entre los gurúes del momento es Valdis Krebs, quien ha examinado a la luz de estas ideas la problemática de identificar la organización de Al Qaeda. No implico que este personaje Krebs encarne el ejemplo a seguir, ni que las ciencias sociales puedan devenir un nuevo semillero de oráculos, pero lo cierto es que estamos más cerca que antes de comprender algunas claves que pueden resultar importantes en el corto plazo. Esta nueva comprensión, concomitante a nuevas posibilidades prácticas, puede servir a los buenos y a los malos usos, como independientemente ha concluido también Jorge Miceli (2008). La figura 28 muestra un ejemplo incluido en Network Workbench ilustrando en forma de grafo radial la red del 11 de setiembre, un recurso pedagógico que al lado del gráfico log-log del número de atentados versus su magnitud se ha tornado habitual en ensayos y piezas de software, y que no estoy seguro de saber cómo interpretar (cf. Clauset y Young 2005; Clauset, Young y Gleditch 2007; Johnson y otros 2006). Cada quien decidirá qué carácter darle y a qué propósito servir con la nueva ciencia, en una dimensión que constituye, yendo un poco más allá de la quincena planeada al principio del ensayo, la lección epistemológica y el desafío del conocimiento más importante de los que hemos discutido hasta ahora. Referencias bibliográficasAiello, Marco, Ian E. Pratt-Hartmann y Johan F. A. K. van Benthem (compiladores). 2007. Handbook of spatial logics. Dordrecht, Springer. Amaral, L. A. N. y J. M. Ottino. 2004. “Complex networks: Augmenting the framework for the study of complex systems”. European Physical Journal B, 38: 147-162. Arrow, Kenneth. 1950. “A difficulty in the concept of social welfare”. Journal of Political Economy, 58(4): 328-346. Austin, T. L., R. E. Fagen, W. F. Penney y John Riordan. 1959. “The number of components of random linear graphs”, Annals of Mathematical Statistics, 30: 747-754. Bak, Per. 1994. “Self-organized criticality: A holistic view of nature”. En: G. Cowan, D. Pines y D. Meltzer (compiladores), Complexity: Metaphors, Models, and Reality, Santa Fe Institute Studies in the Sciences of Complexity, Vol. 19, Reading, Addison-Wesley, pp. 477–495. Bak, Per. 1996. How Nature Works: The Science of Self-Organized Criticality. Nueva York, Springer. Bak, Per y Kan Chen. 1991. “Self-organized criticality”. Scientific American, 264(1): 46–53. Barabasi, Albert-László y Réka Albert. 1999. “Emergence of scaling in random networks”. Science, 286(5440): 509–512. Barabási, Albert-László. 2003. Linked: How everything is connected to everything else and what it means. Nueva York, Plume Books. Barabási, Albert-László y Eric Bonabeau. 2003. “Scale-free networks”. Scientific American, 288(5): 50-59. Barnes, John. 1954. “Class and Committees in a Norwegian Island Parish”. Human Relations, 7(1): 39-58. Barnes, John. 1969. “Networks and political processes”. En: J. C. Mitchell (compilador), Op. cit., pp. 51-76. Barnes, John. 1972. Social networks. Module in Anthropology nº 26. Reading, Addison-Wesley. Barth, Fredrik. 1992. “Towards greater naturalism in conceptualizing society”. En: A. Kuper (compilador), Conceptualizing society. Londres, Routledge, 17-33. Bateson, Gregory. 1980. Espíritu y naturaleza. Buenos Aires, Amorrortu. Bavelas, Alexander. 1948. “A mathematical model for group structures”. Applied Anthropology, 7(1): 16-30. [Traducción castellana: “Un modelo matemático para las estructuras del grupo”. En: Alfred G. Smith (compilador), Comunicación y cultura, vol. 2, Buenos Aires, Nueva Visión, 1977, pp. 91-98]. Bavelas, Alexander. 1950. “Communication patterns in task orientated groups”. Journal of the Acoustical Society of America, 22: 271–288. Bender-deMoll, Skye y Daniel A. McFarland. 2006. “The art and science of dynamic network visualization”. Journal of Social Structure, 7(2), http://www.cmu.edu/joss/content/articles/volume7/deMollMcFarland. Berge, Claude. 1991. Graphs. 3a edición revisada, Amsterdam, North Holland. Berkowitz, Stephen. 1982. An introduction to structural analysis: The network approach to social research. Toronto, Butterworth. Bertuglia, Cristoforo Sergio y Franco Vaio. 2005. Nonlinearity, chaos, and complexity: The dynamics of natural and social systems. Oxford, Oxford University Press. Blair, D. y R. Pollack. 1999. “La logique du choix collectif”. Pour la Science – Dossier: Les mathématiques sociales, Julio, pp. 82-89. Boccaletti, Stefano, Vito Latora, Yamir Moreno, Mario Chavez, Dong-Uk Hwang. 2006. “Complex networks: Structure and dynamics”. Physics Reports, 424: 175-308. Boissevain, Jeremy. 1979. “Network analysis: A reappraisal”. Current Anthropology, 20(2): 392-394. Bollobás, Béla. 2001. Random graphs. 2a edición, Cambridge, Cambridge University Press. Bollobás, Béla. 2002. “The Erdös-Rényi theory of random graphs”. En Gábor Halász, László Lovász, Miklós Simonovits y Vera Sós (compiladores), Paul Erdös and his mathematics II. Berlín, Springer. Bollobás, Béla y Oliver Riordan. 2003. “Mathematical results on scale-free random graphs”. En: S. Bornholdt y H. G. Schuster (compiladores), Op. cit., pp. 1-34. Bollobás, Béla y Oliver Riordan. 2006. Percolation. Cambridge, Cambridge University Press. Bondy, John Adrian y U. S. R. Murty. 1976. Graph theory with applications. Nueva York, North-Holland. Borgatti, Steven y Martin Everett. 2006. “A graph-theoretic perspective in centrality”. Social Networks, 8(4): 466-484. Borgatti, Steve, Martin Everett y Linton Clarke Freeman. 2002. Ucinet for Windows: Software for Social Network Analysis. Harvard, Analytic Technologies. Bornholdt, Stefan y Hans Georg Schuster (compiladores). 2003. Handbook of graphs and networks. From the genome to the Internet. Weinheim, Wiley. Boschetti, Fabio, John Finnigan, Philip Valencia, Ian Enting, J. German y David Neuth. 2004. “Does anything emerge?”. Manuscrito inédito. http://www.citeulike.org/group/2050/article/1282727. Bott, Elizabeth. 1957. Family and Social Network. Londres, Tavistock. Bott, Elizabeth. 1971. Family and Social Network. 2a edición, Londres, Tavistock. Bouquet, Mary. 1993. Reclaiming british kinship: Portuguese refractions of british kinship theory. Manchester, Manchester University Press. Bouquet, Mary. 2001. “Genealogy in anthropology”. En: N. Smelser y P. Baltes, Op. cit., pp. 6029-6032. Brandes, Ulrik y Thomas Erlebach (compiladores). 2005. Network analysis: Methodological foundations. Berlín, Springer Verlag. Breiger, Ronald, Kathleen Carley y Philippa Pattison (compiladores). 2003. Dynamic social networks modeling and analysis. Washington, Committee of Human Factors, National Research Council. Broadbent, Simon R. y John Michael Hammersley. 1957. “Percolation processes, 1. Crystals and mazes”. Proceedings of the Cambridge Philosophical Society, 53: 629–641. Brooks, Frederick. 1975. The mytical man-month: Essays on software engineering. Reading, Addison-Wesley. Camazine, Scott, Jean-Louis Deneubourg, Nigel Franks, James Sneyd, Guy Theraulaz y Eric Bonabeau. 2003. Self-organization in biological systems. Princeton, Princeton University Press. Caplow, Theodore. 1974. Dos contra uno: Teoría de coaliciones en las tríadas. Madrid, Alianza. Cardy, John. 1996. Scaling and renormalization in statistical physics. Cambridge, Cambridge University Press. Carsten, Janet. 2004. After kinship. Cambridge, Cambridge University Press. Cartwright, Dorwin y Frank Harary. 1956. “Structural balance: A generalization of Heider’s theory”. Psychological Review, 63: 277-292. Chapple, Eliot. 1940. “Measuring human relations: an introduction to the study of the interaction of individuals”. Genetic Psychology Monographs, 22(1): 3–147. Chapple, Eliot. 1953. Discussion, “Patterns in biology, linguistics, and culture”. En: S. Tax y otros (compiladores), An Appraisal of Anthropology Today, Chicago, Chicago University Press, pp. 299-321. Chiesi, Antonio M. 2001. “Network analysis”. En: N. Smelser y P. Baltes, Op. cit., pp. 10499-10502. Christen, Markus y Laura Rebecca Franklin. 2002. “The concept of emergence in complexity science: Finding coherence between theory and practice”. Proceedings of the SFI Complex Systems Summer School, 2002. http://www.ini.uzh.ch/~markus/articles/Emergence_def.pdf. Accesado en setiembre de 2007. Clauset, Aaron y Maxwell Young. 2005. “Scale invariance in global terrorism”. arXiv:physics/0502014v2, http://arxiv.org/abs/physics/0502014v2. Accesado en febrero de 2008. Clauset, Aaron, Maxwell Young y Kristian Skrede Gleditsch. 2007. “On the frequency of severe terrorist events”. Journal of Conflict Resolution, 51(1): 51-88. Cohen, Jack e Ian Stewart. 1994. The collapse of chaos: Discovering simplicity in a complex world. Nueva York, Penguin. Collard, Chantal. 2000. “‘Kinship studies’ au tournant du siècle”. L’Homme, 154-155: 635-658 Corominas-Murtra, Bernat, Sergi Valverde y Ricard Solé. 2007. “The ontogeny of scale-free syntax networks through language acquisition”. Santa Fe Institute, Working Papers 07-06-012, http://www.santafe.edu/research/publications/workingpapers/07-06-012.pdf. Courrège, Philippe. 1965. “Un modèle mathématique des structures élémentaires de parenté”. L’Homme, 5(3-4): 248-290. Crutchfield, James. 1994. “Is anything ever new? Considering emergence”. En: G. Cowan, D. Pines, y D. Melzner (compiladores), Santa Fe Institute Studies in the Sciences of Complexity, XIX, Reading, Addison-Wesley. Csermely, Péter. 2006. Weak links: Stabilizers of complex systems from proteins to social networks. Nueva York, Springer. D’Andrade, Roy. 2000. “The sad story of anthropology 1950-1999”. Cross-cultural research, 34(3): 219-232. Davidson, Ron y David Harel. 1996. “Drawing graphs nicely using simulated annealing”. ACM Transactions on Graphics, 15(4): 301-331. De Nooy, Wouter, Andrej Mrvar y Vladimir Batagelj. 2005. Exploratory network analysis with Pajek. Cambridge, Cambridge University Press. Di Battista, Giuseppe, Peter Eades, Roberto Tamassia, Ioannis Tollis. 1999. Graph drawing: Algorithms for the visualization of graphs. Upper Saddle River, Prentice Hall. Diestel, Reinhard. 2000. Graph theory. Nueva York, Springer-Verlag. Dorogovtsev, Sergey N. y José Fernando Ferreira Mendes. 2001. “Language as an evolving word web”. Proceedings of the Royal Society of London B, 268(1485): 2603-2606. Durrett, Rick. 2007. Random graph dynamics. Cambridge, Cambridge University Press. Edgar, Gerald. 2008. Measure, topology, and fractal geometry. Nueva York, Springer Science+Business Media. Erdös, Paul. 1973. The art of counting: Selected writings. Cambridge (USA), The MIT Press. Erdös, Paul. 1989. “Distances with specifed multiplicities”. American Mathematical Monthly, 96: 447. Ericksen, Eugene y William Yancey. 1977. “The locus of strong ties”. Manuscrito inédito, Universidad de Temple. Euler, Leonhard. 1741. “Solutio problematis ad geometriam sitvs pertinentis”. Comentarii Academiae Scientiarum Petropolitanae, 8: 128-140. [Traducción al inglés: “Los siete puentes de Königsberg”. En: James Newman (compilador), The world of mathematics, Redmond, Tempus Books, 1988, vol. 1, pp. 565-571]. http://www.math.dartmouth.edu/~euler/docs/originals/E053.pdf. Evans, Merran, Nicholas Hastings y Brian Peacock. 1993. Mathematical distributions. 2a edición, Nueva York, John Wiley & Sons. Fáth, Gábor y Miklos Sarvary. 2005. “A renormalization group theory of cultural evolution”. Physica A, 348: 611-629. Fogelson, Raymond. 2001. “Schneider confronts componential analysis”. En: Richard Feinberg y Martin Ottenheimer, The cultural analysis of kinship: The legacy of David M. Schneider. Urbana, University o Illinois Press, pp. 33-45. Foster, Brian y Stephen Seidman. 1981. “Network structure and the kinship perspective”. American Ethnologist, 8(2): 329-355. Franzén, Torkel. 2005. Gödel’s theorem: An incomplete guide to its use and abuse. Massachusetts, A. K. Peters. Freeman, Linton Clarke. 1982. “Centered graphs and the structure of ego networks”. Mathematical Social Sciences, 3: 291-304. Freeman, Linton Clarke. 1984. “Turning a profit from mathematics: The case of social networks”. Journal of Mathematical Sociology, 10: 343-360. Freeman, Linton Clarke. 2000. “Visualizing social networks”. Journal of Social Structure, 1, http://www.cmu.edu/joss/content/articles/volume1/Freeman.html. Freeman, Linton Clarke. 2004. The development of social network analysis: A study in the sociology of science. Vancouver, Booksurge Publishing. Friedkin, Noah. 2003. “Social influences network theory: Toward a science of strategic modification of interpersonal influence systems”. En: R. Breiger y otros (compiladores), Op. cit., pp. 89-100. Fruchterman, Thomas y Edward Reingold. 1991. “Graph drawing by force-directed placement”. Software – Practice and Experiencie, 21(1): 1129-1164. Gadamer, Hans-Georg. 1977 [1960]. Verdad y método. Salamanca, Sígueme. Gardner, Martin. 1988. La ciencia: Lo bueno, lo malo y lo falso. Madrid, Alianza. Garey, Michael y David Johnson. 1979. Computers and intractability: A guide to the theory of NP-completeness. San Francisco, H. W. Freeman and Company. Geertz, Clifford. 1987 [1973]. La interpretación de las culturas. México, Gedisa. Geertz, Clifford. 2000. Available light. Anthropological reflections on philosophical topics. Princeton, Princeton University Press. Gilbert, E. N. 1959. “Random graphs”. Annals of Mathematical Statistics 30: 1141–1144. Goodman, Nelson. 1972. Problems and projects. Nueva York, Bobbs Merrill. Granovetter, Mark. 1973. “The strength of weak ties”. American Journal of Sociology, 78: 1360-1380. Granovetter, Mark. 1983. “The strength of weak ties: A network theory revisited”. Sociological Theory, 1: 201-233. Granovetter, Mark. 1985. “Economic action and social structure: The problem of embeddedness”. American Journal of Sociology, 91: 481-510. Granovetter, Mark. 1990. “The myth of Social Network Analysis as a special method in the social sciences”, Conferencia Magistral, Sunbelt Social Networks Conference, San Diego, 15 de febrero, Connections, 13(1-2): 13-16. Grimmett, Geoffrey. 1999. Percolation. 2ª edición, Berlín y Heidelberg, Springer. Grupo Anthropocaos (Jorge Miceli, Diego Díaz, Sergio Guerrero, Damián Castro, Mora Castro, Ramón Quinteros, Jordan Kristoff, Ignacio García). 2007. Exploraciones en Antropología y Complejidad, Buenos Aires, Editorial Sb. Hadamard, Jacques. 1902. “Sur les problèmes aux dérivées partielles et leur signification physique”. Princeton University Bulletin, 13(1): 49-52. Hage, Per. 1979. “Graph theory as a structural model in cultural anthropology”. Annual Review of Anthropology, 8: 115-136. Hannerz, Ulf. 1986 [1980]. Exploración de la ciudad: Hacia una antropología urbana. México, Fondo de Cultura Económica. Harary, Frank. 1969. Graph theory. Reading, Addison-Wesley. Hatcher, Melanie y Chris Tofts. 2004. “Reductionism isn’t functional”. Hewlett-Packard Technical Reports, HPL-2004-222. Hayes, Brian. 2002. “Statistics of deadly quarrels”. American Scientist, 90(1): 10-15. Herrnstein, Richard y Charles Murray. 1994. The bell curve: Intelligence and class structure in American life. Nueva York, Free Press. Hopcroft, John E. y Robert E. Tarjan. 1974. “Efficient planarity testing”. Journal of the ACM, 21(4): 549-568. Hopcroft, John Edward, Rajeev Motwani y Jeffrey Ullman. 2001. Introduction to automata theory, languages and computation. 2a edición. Reading, Addison-Wesley. Hudson Richard. 2006. Language Networks: The New Word Grammar. Nueva York, Oxford University Press. Isaac, Barry. 2005. “Karl Polanyi”. En: James Carrier (compilador), A handbook in economic anthropology. Cheltenham, Edward Elgar, pp. 14-25. Janson, Svante, Tomasz Łukzac y Andrzej Rucinski. 2000. Random graphs. Nueva York, John Wiley & Sons. Jensen, Henrik Jeldtoft. 1998. Self-organized criticality: Emergent complex behavior in physical and biological systems. Cambridge, Cambridge University Press. Johnson,
Neil, Mike Spagat, Jorge Restrepo, Oscar Becerra, Juan Camilo
Bohórquez, Nicolás Suárez, Elvira María
Restrepo y Roberto Zarama. 2006. “Universal
patterns underlying ongoing wars and terrorism”.
oai:arXiv.org:physics/0605035, http://www.citebase.org/fulltext?format=application%2Fpdf&identifier=oai%3 Kadanoff, Leo. 1983. “Roads to chaos”. Physics Today, diciembre, 36: 46-53. Kadanoff, Leo. 1999. From order to chaos II: Essays: Critical, chaotic and otherwise. Nueva York, World Scientific Publishing Company. Kapferer, Bruce. 1969. “Norms and the manipulation of relationships in a work context”: En: J. C. Mitchell (compilador), Op. cit., 181-244. Kapferer, Bruce. 1972. Strategy and transaction in an African factory: African workers and Indian management in a Zambian town. Manchester, Manchester University Press. Kapferer, Bruce. 1973. “Social network and conjugal role in urban Zambia: Towards a reformulation of the Bott hypothesis”. En: Jeremy Boissevain & J. Clyde Mitchell, Network Analysis Studies in Human Interaction. La Haya, Mouton & Co. Klau, Gunnar y René Weiskircher. 2005. “Robustness and resilience”. En: U. Brandes y T. Erlebach (compiladores), Op. cit., cap. §15, pp. 417-437. Kleiber, Christian y Samuel Kotz. 2003. Statistical size distribution in economics and actuarial sciences. Hoboken, Wiley Interscience. Kleinfeld, Judith. 2002. “The small world problem”. Society, 39(2): 61-66. König, Dénes. 1931. “Gráfok és mátrixok”. Matematikai és Fizikai Lapok, 38: 116–119. Krishnamoorty, Kalimuthu. 2006. Handbook of statistical distributions with applications. Boca Raton, Chapman & Hall / CRC. Kochen, Manfred & Ithiel de Sola Pool. 1978. “Contacts and influence”. Social Networks, 1(1): 1-51. Kolata, Gina. 1998. “Scientific myths that are too good to die”. The New York Times, 6 de diciembre. Kubík, Aleš. 2003. “Toward a formalization of emergence”. Artificial Life, 9: 41-65. Kuper, Adam. 2003. “What really happened to kinship and kinship studies”. Journal of Cognition and Culture, 3(4): 329-335. Lamphere, Louise. 2001. “Whatever happened to kinship studies?: Reflections of a feminist anthropologist”. En: Linda Stone (compiladora), New directions in anthropological kinship, Lanham, Rowman & Littlefield. Landsberger, Henry. 1958. Hawthorne revisited. Ithaca, Cornell Social Science Research Center. Laville, Jean-Louis. 2007. “The social dimension of the economy according to Mark Granovetter”. Sociologica, 2, doi: 10.2383/24768. http://www.sociologica.mulino.it/doi/10.2383/24768, accesado febrero de 2008. Leinhardt, Samuel. 1977. Social Networks: A developing paradigm. Nueva York, Academic Press. Lévi-Strauss, Claude. 1985 [1949]. Las estructuras elementales del parentesco. Barcelona, Planeta-Agostini. Lévi-Strauss, Claude. 1973 [1958]. Antropología estructural. 5ª edición, Buenos Aires, Eudeba. Liljeros, Fredrik, Christopher Edling y Luis Nunez Amaral. 2003. “Sexual networks: Implications for the transmission of sexually transmitted infections”. Microbes and Infection, 5: 189-196. Lin, Nan, W. Ensel y J. Vaughn. 1981. “Social Resources, Strength of Ties and Occupational Status Attainment”. American Sociological Review 46(4): 393-405. Lomnitz, Larissa. 1974. Networks and marginality. Nueva York, Academic Press. Lorrain, François y Harrison C. White. 1971.“Structural equivalence of individuals in social networks”. Journal of Mathematical Sociology, 1: 49-80. Mandelbrot, Benoît. 1967. “How long is the coast of Britain?: Self-similiarity and fractional dimension”. Science, 156(3775): 636-638. Mandelbrot, Benoît y Richard L. Hudson. 2006. Fractales y finanzas: Una aproximación matemática a los mercados. Barcelona, Tusquets. Martino, Francesco y Andrea Spoto. 2006. “Social networks analysis: A brief theoretical review and further perspectives in the study of intormation technology”. PsychNology Journal, 4(1): 53-86. Masucci, Adolfo. P. y Geoff J. Rodgers. 2006. “Network properties of written human language”, http://arxiv.org/PS_cache/physics/pdf/0605/0605071v1.pdf. Consultado marzo de 2008. Mayer, Philip. 1961. Tribesmen on townsmen: Conservatism and the process of urbanization in a South African city. Capetown, Oxford University Press. McMahon, David. 2006. Linear algebra demystified. Nueva York, McGraw Hill. McNeal, Edward. 1994. MathSemantics: Making numbers talk sense. Londres, Penguin. Mel’čuk, Igor. 1985. Dependency syntax. Albany, SUNY Press. Mel’čuk, Igor. 2003. “Levels of dependency in linguistic description: Concepts and problems”. En: V. Agel, L. Eichinnger, H.-W. Eroms, P. Hellwig, H. J. Herringer y H. Lobin (compiladores), Dependency and Valency. An International Handbook of Contemporary Research, vol. 1. Berlín - Nueva York, Walter de Gruyter, pp. 188-229. Merton, Robert. 1968. “The Matthew effect in science”. Science, 159(3810): 56-63. Miceli, Jorge. 2007. “Modelos de percolación y difusión de ideas en ciencias sociales: Una clasificación provisoria”. En: Grupo Antropocaos, Exploraciones en Antropología y Complejidad. Buenos Aires, Editorial Sb, pp. 67-104. Miceli, Jorge. 2008. “Problemas de validez en el análisis de las redes sociales: Algunas reflexiones integradoras”, en C. Reynoso (editor), Críticas y modelos heterodoxos en antropología compleja. Buenos Aires, Editorial Sb. Miceli, Jorge y Sergio Guerrero. 2007. “Redes libres de escala y su uso en el análisis de datos etnográficos: El caso de la comunidad Tehuelche del Chalía”. En: Grupo Antropocaos, Exploraciones en Antropología y Complejidad. Buenos Aires, Editorial Sb, pp. 177-191. Mika, Stephen. 2007. Social networks and the semantic web. Nueva York, Springer Science. Milgram, Stanley. 1967. “The small world problem”. Psychology Today, 1(1): 61-67. Mitchell, James Clyde (compilador). 1969. Social Networks in Urban Settings. Manchester, Manchester University Press. Mitchell, James Clyde. 1974. “Social networks”. Annual Review of Anthropology, 3: 279-299. Mitchell, Melanie. 2006. “Complex systems: Network thinking”. SFI Working Papers, 06-10-036. http://www.santafe.edu/research/publications/workingpapers/06-10-036.pdf Moreno, Jacob Levy. 1932. Application of the Group Method to Classification. Nueva York, National Committee on Prisons and Prison Labor. Moreno, Jacob Levy. 1953 [1934]. Who Shall Survive? Foundations of sociometry, group psychotherapy and sociodrama. Beacon, Beacon House Inc. Moreno, Jacob Levy y Helen Hall Jennings. 1938. “Statistics of social configurations”. Sociometry 1: 342–374. Morin, Edgar. 1998b [1991]. El Método. IV. Las ideas. 2ª edición, Madrid, Cátedra. Morin, Edgar. 2003 [1990]. Introducción al pensamiento complejo. Barcelona, Gedisa. Nadel, Siegfried. 1957. The theory of social structure. Londres, Cohen and West. Nadel, Siegfried. 1974 [1951]. Fundamentos de antropología social. 2ª reimpresión en español, México, Fondo de Cultura Económica. Needham, Rodney. 1971. “Remarks on the analysis of kinship and marriage”. En: Rethinking kinship and marriage, Londres, Tavistock, pp. 1-43. Newman, Mark E. J. 2003. “Structure and function of complex networks”. arXiv:cond-mat/0303516 v1 Nishizeki, Takao y Md. Saidur Rahman. 2004. Planar graph drawing. Singapur, World Scientific Publishing Co. Ore, Oystein. 1962. Theory of graphs. Providence, American Mathematical Society. Paczuski, Maya. 2005. “Networks as renormalized modelsfor emergent behavior in physical systems”, arXiv:physics/0502028v1, http://arxiv.org/abs/physics/0502028v1. Pala, Gergely, Imre Derényi, Illés Farkas y Tamás Vicsek. 2005. “Uncovering the overlapping community structure of complex networks in nature and society”. ArXiv:physics/0506133v1, http://it.arxiv.org/abs/physics/0506133v1. Peletz, Michael. 1995. “Kinship studies in late twentieth-century anthropology”. Annual Review of Anthropology, 24: 343-372. Pérez-Taylor, Rafael. 2006. Anthropologias: Avances en la complejidad humana. Buenos Aires, Editorial Sb. Platt, Jennifer. 1969. “Some problems in measuring the jointness of conjugal role relationship”. Sociology, 3(3): 287-297. Rachev, S. T. 2003. Handbook of heavy tailed distributions in finance. Amsterdam, Elsevier/North Holland. Radcliffe-Brown, Alfred Reginald. 1965 [1952]. Structure and function in primitive society. Nueva York, Free Press – Macmillan. Rapoport, Anatol. 1957. “Contribution to the theory of random and biased nets”. Bulletin of Mathematical Biophysics, 19: 257–277. Read, Dwight. 2001. “Formal analysis of kinship terminologies and its relationship to what constitutes kinship”. Anthropological Theory, 1(2): 239-267. Read, Dwight y Cliffors Behrens. 1990. “KAES: An expert system for the algebraic analysis of kinship terminologies”. Journal of Quantitative Anthropology, 2: 353-393. Reilly, William J. 1931. The law of retail gravitation. Nueva York, G. P. Putnam & Sons. Reynoso, Carlos. 2006. Complejidad y Caos: Una exploración antropológica. Buenos Aires, Editorial Sb. Reynoso, Carlos. 2008. Corrientes teóricas en antropología: Perspectivas para el tercer milenio. Buenos Aires, Editorial Sb. Richards, William y Andrew Seary. 1997. “Introduction to eigen analysis of networks”. INSNA Sunbelt XVII. San Diego, febrero, http://www.sfu.ca/~richards/Pages/wdr97.htm. Richardson, Lewis Fry. 1948. “Variation of the frequency of fatal quarrels with magnitude”. Journal of the American Statistical Asociation, 43: 523. Richardson, Lewis Fry. 1961. “The problem of contiguity: An appendix of statistics of deadly quarrels”. General System Yearbook, 6: 139-187. Roethlisberger, Fritz y W. J. Dickson. 1939. Management and the worker. Cambridge (USA), Harvard University Press. Rosen, Robert. 2000. Essays on life itself. Nueva York, Columbia University Press. Rouse Ball, Walter William. 1892. Mathematical recreations and problems of past and present times. Londres, Macmillan. Schneider, David. 1984. A critique of the study of kinship. Ann Arbor, University of Michigan Press. Schweizer, Thomas. 1996. “Reconsidering social networks: Reciprocal gift exchange among the !Kung”. Quantitative Anthropology, 6(1-4): 147-170. Schweizer, Thomas. 1997. “Embeddedness of ethnographic cases: A social networks perspective”. Current Anthropology, 38(5): 739-760. Scott, John. 2000. Social network analysis: A handbook. 2a edición, Londres, Sage Publications. Seary, Andrew y William Richards. 2003. “Spectral methods for analyzing and visualizing networks”. En: R. Breiger y otros, Op. cit., pp. 209-228. Segalen Martine y Claude Michelat. 1991. “L’amour de la généalogie”. En: M. Segalen (compiladora), Jeux de Famille. París, Presses de CNRS, pp. 193–208. Segarra, José Gabriel. 2001. Vida artificial: Del caos al orden. Guía práctica de la complejidad. Alzira, Algar Editorial. Shalizi, Cosma y Christopher Moore. 2003. “What is a macrostate? Subjective observations and objective dynamics”. http://arxiv.org/PS_cache/cond-mat/pdf/0303/0303625v1.pdf. Accesado en setiembre de 2007. Shores, Thomas. 2007. Applied linear algebra and matrix analysis. Nueva York, Springer Science+Business Media. Simmel, Georg. 1966 [1922]. Conflict and the web of group affiliations. Nueva York, Free Press. Smelser, Neil y Paul Baltes (compiladores). 2001. International Encyclopedia of the Social and Behavioral Sciences. Oxford, Elsevier. Solé, Ricard, Bernat Corominas Murtra, Sergi Valverde y Luc Steels. 2005. “Language networks: Their structure, function, and evolution”. SFI Working papers, 05-12-042, http://www.santafe.edu/research/publications/workingpapers/05-12-042.pdf. Sornette, Didier. 2006. Critical phenomena in the natural sciences: Chaos, fractals, selforganization and disorder. Concepts and tools. 2a edición, Berlín-Heidelberg, Springer. Sousa, Paulo. 2003. “The fall of kinship: Towards an epidemiological explanation”. Journal of Cognition and Culture, 3(4): 265-303. Sperber, Dan. 1994. “The modularity of thought and the epidemiology of representations”. En: L. A. Hirschfeld y S. A. Gelman (compiladores), Mapping the mind: Domain specificity in Cognition and Culture. Nueva York, Cambridge University Press, pp. 39-67. Sperber, Dan. 1996. Explaining culture: A naturalistic approach. Oxford, Blackwell. Sperber, Dan. 2000. “Why memes won’t do”. En: R. Aunger (compilador), Darwinizing culture. The status of memetics as a science. Oxford, Oxford University Press, pp. 163-174. Sperber, Dan y Deirdre Wilson. 1986. Relevance: Communication and cognition. Oxford, Blackwell. Stack, Carol. 1974. All our kin. Nueva York, Harper & Row. Stauffer, Dietrich y Amnon Aharony. 1994. Introduction to percolation theory. 2a edición, Londres, Taylor and Francis. Steyer, Alexandre and Jean-Benoît Zimmermann. 2000. “Self Organised Criticality in Economic and Social Networks: The case of innovation diffusion”. En: Alan Kirman y J.-B. Zimmermann (compiladores), Economics with Heterogeneous Interacting Agents, Berlín, Springer. Strang, Gilbert. 1988. Linear algebra and its applications. 3a edición, South Melbourne, Thomson Learning. Strogatz, Steven. 2003. Sync: The emerging science of spontaneous order. Nueva York, Hyperion Books. Swedberg, Richard. 1990. Economics and sociology. Princeton, Princeton University Press. Swedberg, Richard. 2000. “Economic sociology”. En: Edgar Borgatta y Rhonda Montgomery (compiladores), Encyclopedia of Sociology, 2ª edición, Nueva York, Macmillan Reference, vol. 2, pp. 731-741. Tamassia, Roberto. 1997. “Graph Drawing”. En: J. E. Goodman y J. O’Rourke (compiladores), Handbook of Discrete and Computational Geometry. Boca Ratón y Nueva York, CRC Press, pp. 815-832. Tamassia, Roberto. 1999. “Advances in the theory and practice of graph drawing”. Theoretical Computer Science, 217(2): 2335-254. Tamassia, Roberto. 2000. “Graph drawing”. En: J.-R. Sack y J. Urrutia (compiladores), Handbook of computational geometry. Amsterdam, Elsevier Science, pp. 937-972. Tarantola, Albert. 2005. Inverse problem theory and nethods for model parameter estimation. Filadelfia, SIAM (Society for Industrial and Applied Mathematics). Thom, René. 1992. “Determinismo e innovación”. En: J. Wagensberg (compilador), Op. Cit., pp. 63-78. Thurman, Blake. 1980. “In the office: Networks and coalitions”. Social Networks, 2(1): 47-63. Toussaint, Godfried. 2005. “The geometry of musical rhythm”. Research report. School of Computer Science, McGill University. Travers, Jeffrey y Stanley Milgram. 1969. “An experimental study of the Small World poblem”. Sociometry, 32(4): 425-44. Turner, Christopher. 1967. “Conjugal roles and social networks: An examination of an hypothesis”. Human Relations, 20(2): 121-130. Voss, Richard F. y John Clarke. 1975. “1/f noise in music and speech”. Nature, 258: 317-318. Wagensberg, Jorge (compilador). 1992. Proceso al azar. 2ª edición, Barcelona, Tusquets. Wang, Xiao Fan y Guanrong Chen. 2003. “Complex networks: Small-world, scale-free and beyond”. IEEE Systems and Circuits Magazine, primer trimestre, pp. 6-20. Warner, William Lloyd. 1931. “Morphology and functions of the Australian Murngin type of kinship (Part I)”. American Anthropologist, 33(2): 172-198. Wasserman, Stanley y Katherine Faust. 1994. Social networks analysis: Methods and applications. Nueva York, Cambridge University Press. Watts, Duncan. 2004. Six degrees: The science of a connected age. Londres, Vintage. Watts, Duncan y Peter Sheridan Dodds. 2007. “Influentials, networks, and public opinion formation”. Journal of Consumer Research, 34: 441-458. Watts, Duncan y Steven Strogatz. 1998. “Collective dynamics of ‘smallworld’ networks”. Nature, 393(6684): 440–442. Weaver, Warren. 1948. “Science and complexity”. American Scientist, 36: 536-644. Weil, André. 1985. “Acerca del estudio algebraico de ciertos tipos de leyes de matrimonio (Sistema Murngin)”. En: C. Lévi-Strauss, Op. cit., pp. 278-284. Weisbuch, Gérard, Sorin Solomon y Dietrich Stauffer. 2003. “Social percolators and self organized criticality”. En: S. Bornholdt y H. G. Schuster (compiladores), Op. cit., pp. 342-354. White, Douglas R. 2001. “Network analysis and social dynamics”. Universidad de California en Irvine, Manuscrito. White, Douglas R. y Paul Jorion. 1992. “Representing and computing kinship: A new approach”. Current Anthropology, 33(4): 454-462. White, Harrison, Scott A. Boorman y Ronald L. Breiger. 1976. “Social Structure from Multiple Networks. I. Blockmodels of Roles and Positions”. The American Journal of Sociology, 81(4): 730-780. Whitten, Norman y Alvin Wolfe. 1973. “Network analysis”. En: John Honigmann (compilador), Handbook of social and cultural anthropology. Chicago, Rand McNally, pp. 716-746. Wilson, Alan G. 1967. “A Statistical Theory of Spatial Distribution Models”. Transportation Research, 1: 253–269. Wilson, Alan G. 1970. Entropy in Urban and Regional Modelling. Londres, Pion. Wilson, Alan G. 1974. Urban and Regional Models in Geography and Planning. Londres, Wiley. Wilson, Robin. 2004. “History of graph theory”. En: Jonathan Gross y Jay Yellen (compiladores), Handbook of graph theory. Boca Raton, CRC Press. Wolfe, Alvin. 1978. “The rise of network thinking in anthropology”. Social Networks, 1(1): 63-74. Wolfe, Alvin. 1997. Reseña de Social network analysis de S. Wasserman y K. Faust. American Ethnologist, 24(1): 219-220. Wolff, Kurt. 1950. The sociology of Georg Simmel. Glencoe, The Free Press. Referencias tecnológicasAdit Sociogram. © s/fecha, Adit Limited. http://www.aditsite.co.uk/more20.htm#Adit%20Sociogram. Consultado 28 de enero de 2008. Agna. V. 2.1.1, (Applied Graph & Network Analysis) © 2002-2003 A. M. Benta, 12 de diciembre de 2003. http://www.geocities.com/imbenta/agna. Consultado 26 de enero de 2008. Network Workbench Tool, v. 0.9.0 © 2005 University of Indiana, 26 de febrero de 2008. http://nwb.slis.indiana.edu/index.html. Consultado 26 de febrero de 2008. Pajek, v. 1.22, © 1996-2008, Vladimir Batagelj & Andrej Mrvar, 16 de enero de 2008. http://vlado.fmf.uni-lj.si/pub/networks/pajek/. Consultado 28 de enero de 2008. Visone v. 2.3.3 © 2001-2008 Visone Project Team. NOTAS1 Los paradigmas de la complejidad de Edgar Morin o de Fritjof Capra, la autopoiesis, el constructivismo radical, la cibernética de los sistemas observadores y la investigación social de segundo orden, la concepción posmoderna de la complejidad. Véase Reynoso (2006: 112-160, 174-192). 2 No por casualidad John E. Hopcroft es el mismo autor que desarrolló junto con Robert Tarjan un algoritmo de tiempo lineal para determinar si un grafo puede ser planar (o linear), esto es, si se puede dibujar de tal modo que sus vínculos no se crucen (Hopcroft y Tarjan 1974; Nishizeki y Rahman 2004: 4). Hopcroft y Tarjan han sido ambos ganadores del prestigioso Premio Turing en 1986. El legendario libro de Hopcroft, Motwani y Ullman es conocido en el ambiente como el “Libro Cenicienta” por su curiosa ilustración de portada; pero mil veces he escrutado la portada y no he logrado distinguir el personaje. Una leyenda urbana, tal vez. 3 Conforme lo expresaba René Thom, este conjunto no es otra cosa que una teoría: un modelo (siempre algorítmico, pues aún en hermenéutica hay operadores) más una interpretación empírica (Wagensberg 1992: 201). 4 La vez que estuve un día calendario en Kaliningrado, enclavada en ese jirón de Rusia separada del resto del territorio por los países bálticos, quise conocer los siete puentes originales, pues no hay otra cosa que pueda hacerse allí un domingo por la tarde. Por desdicha no quedaba casi nada de ellos (véase figura 2); en 1944 gran parte de la ciudad vieja ocupada por los nazis fue demolida por los bombardeos ingleses por necesidad imperiosa, pero sin cuidado alguno por lo que hoy llamaríamos la puesta en valor del patrimonio histórico. 5 Por cierto que la inducción existe, que es difícil evitar efectos colaterales y que hay que tener en cuenta esas cuestiones; pero considerar que ése es un escollo mayor denota, después de tanto batir el parche de la reflexividad, una posible falta de imaginación científica. El efecto del observador es órdenes de magnitud más fuerte en mecánica cuántica que lo que sería jamás posible en ciencias sociales; eso no ha impedido en modo alguno el desarrollo de modelos con inédita capacidad de predicción. 6 Brown (Rhode Island), Columbia (Nueva York), Cornell (Ithaca, Nueva York), Darmouth (Hanover, New Hampshire), Harvard (Cambridge, Massachusetts), Princeton (New Jersey), Pennsylvania (Filadelfia), Yale (New Haven, Connecticut). 7 La palabra “evolución” no tiene en este contexto la denotación usual. En la literatura matemática se llama así a la construcción de grafos aleatorios: comenzando con N vértices aislados, el grafo evoluciona (o se desarrolla) mediante el agregado sucesivo de vínculos al azar, 8 Por supuesto, las distribuciones normales (gaussianas) y las de Poisson distan de ser idénticas; no obstante, y siguiendo el principio de Goodman y el ejemplo de Watts (2004: 104) las consideraré aquí suficientemente similares como para incluirlas en la misma familia. 9 De más está decir que no existe ninguna “curva de Bell”, ni tampoco hubo un científico así apellidado que inventara esa criatura epónima. Vale la pena consignar el dato, por si alguien está en camino de reproducir el antipatrón: una bell curve es, sencillamente, una curva en forma de campana. 10 En una presentación sobre redes y complejidad que hice hace un par de años solicité a los asistentes alguna definición de problema que en su trabajo empírico pudiera justificar la presunción de estar técnicamente en condiciones de hallar lo que calificaría como una solución. Como en tantos otros encuentros en las que me aventuré a la misma impertinencia, en esa ocasión nadie levantó la mano. No afirmo que nadie tenga ninguna idea de lo que es un problema, pero sí que no parece haber urgencia por clarificar la cuestión. Por este motivo en este trabajo he hecho explícita esa definición. 11 No es posible aquí definir pedagógicamente cada categoría sin inflar la argumentación más allá de todo control. Será suficiente decir que una máquina de Turing se puede pensar provisoriamente como un conjunto de procedimientos discretos especificables (o algoritmos) que resuelven un problema. 12 Un mito sustantivista más debe caer por tierra. Tras una serie de relecturas de The great transformation, su obra mayor, puedo dar fe que Polanyi nunca utilizó el concepto de embeddedness como nombre. Lo más que llegó a decir es que para los ideólogos del libre mercado “las relaciones sociales están embebidas [embedded] en el sistema económico” (p. 60) y que antiguamente “los motivos y circunstancias de las actividades productivas estaban embebidas en la organización general de la sociedad” (p. 73). Ni una palabra más. 13 Rick Durrett ha demostrado que esas cifras no se sostienen. Si se elimina el 95% de los vínculos Internet sigue conectada, pero suponiendo que la fracción de nodos del componente gigante es 5.9x10-8, si inicialmente estaban conectados seis mil millones de usuarios luego que se eliminen los vínculos sólo 360 podrán consultar su email. El otro resultado depende de que en la distribución de grado se presuma una ley de potencia fija para todos los valores de k, lo que fuerza pk~0.832k-3. Sin embargo, si el grafo se generó mediante un modelo de agregación preferencial con m=2, entonces pk~12k-3, y uno tiene que eliminar el 33% de los hubs (aunque suene drástico se trata de un conjunto de pequeña cardinalidad). Véase Durrett (2007: 1-2, 17-18); Klau y Weiskircher (2005). 14 Para comprender este tema esencial en ciencias sociales en general y estudio de simetrías y ARS en particular, es beneficioso tener una base en álgebra lineal; recomiendo para ello los libros de Gilbert Strang (1988: caps. 5 y 8), David McMahon (2006: caps. 5 y 8) y Thomas Shores (2007: caps. 3 y 5). Sobre eigen-análisis de redes (o sea, métodos espectrales), véase Richards y Seary 1997; Seary y Richards 2003. 15 Benini, Benktander, Bernoulli, Beta, binomial, Cauchy, Champernowne, chi cuadrado, Davis, Dirichlet, Erlang, exponencial, Gumbel, gamma, geométrica, Laplace, logarítmica, lognormal, Gauss, Poisson, Student, von Misses, zeta, de ley de potencia. Cada cual tiene su historia, diagnosis, idiosincracia, significado y etiología. A veces las distribuciones difieren entre sí en pequeño grado; el grano grueso de las mediciones posibles en ciencias sociales (o la impropiedad del diseño algorítmico) casi siempre arroja dudas sobre la distribución que se tiene entre manos. Pero de todos modos las diferentes distribuciones son indicadores significativos, respuestas a la formulación de distintas preguntas, elementos de juicio que ya no es más sensato seguir ignorando.
|
|||||||||||||||||||||
|
|||||||||||||||||||||
